Динамического подобия насосов
При разработке новых конструкций и эксплуатации насосов пользуются законами подобия. Законы подобия дают возможность достаточно точно определить основные параметры проектируемого насоса по известным параметрам модели.
Основное положение теории подобия требует выполнения условий геометрического, кинематического и динамического подобия.
Геометрическое подобие заключается в пропорциональности изменения всех линейных размеров поверхностей, ограничивающих и направляющих поток при сохранении равенства угловых размеров. Математически геометрическое подобие определяется постоянством линейного коэффициента подобия
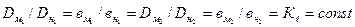 (1.60)
(1.60)
Геометрическое подобие также означает постоянство отношений любых сходственных линейных размеров
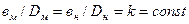 (1.61)
(1.61)
Кинематическое подобие заключается в подобии параллелограммов скоростей в соответствующих точках потока во всех элементах проточной части двух геометрически подобных насосов, работающих в одинаковых режимах. Математически кинематическое подобие можно выразить следующими зависимостями:

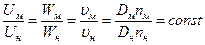 (1.62)
(1.62)
Динамическое подобие предполагает пропорциональность сил, действующих в сходственных точках проточной части, при сохранении геометрического и кинематического подобия. При отнесении к этим силам давления, вязкости, сил тяжести и инерции динамическое подобие означает равенство чисел Эйлера, Рейнольдса, Фруда и Струхаля:
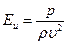 ;
; 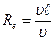 ;
; 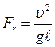 ;
; 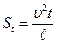 ; (1.63)
; (1.63)
| где | 
| - характерный линейный размер; |
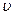
| - кинематическая вязкость жидкости; | |
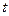
| - время |
Для гидравлических машин при их моделировании важнейшим критерием динамического подобия является равенство чисел Эйлера 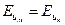 , которое для насосов может быть выражено
, которое для насосов может быть выражено
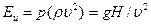

Заменяя скорость пропорциональным отношением подачи к квадрату диаметра рабочего колеса, получим
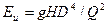 .
.
Тогда
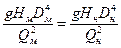 или
или 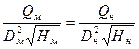 (1.64)
(1.64)
Дата добавления: 2015-07-10; просмотров: 1316;
