Законы подобия насосов

Используя зависимости, выражающие геометрическое подобие насо-сов, получают соотношения технических параметров модели и натуры, т.е. законы подобия.

На основании формулы (1.53), определяющей полезную подачу центробежного насоса, можно установить соотношение подач модели и натуры

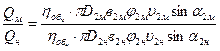
Поскольку рабочие колеса рассматриваемых насосов геометрически подобны, т.е. 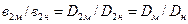и с учетом условий кинематического подобия (1.62), получим

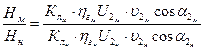
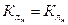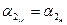Исходя из условий геометрического и кинематического подобия можно считать, что и . С учетом также условий кинематического подобия (1.62) получим

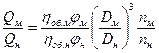, (1.65)

т.е. подача подобных насосов прямо пропорциональна частоте вращения, объемному КПД, коэффициенту стеснения в первой степени и диаметру колеса в третьей степени.

На основании формулы (1.49), определяющей полный напор насоса, можно установить соотношение напоров модели и натуры

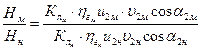
Исходя из условий геометрического и кинематического подобия можно считать, что 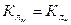и . С учетом также условий кинематического подобия (1.62) получим

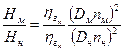, (1.66)

т.е. напор подобных насосов прямо пропорционален гидравлическому КПД в первой степени, произведению диаметра колеса и частоты вращения во второй степени.

Мощность насоса определяется по формуле 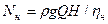, а 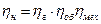. Тогда с учетом выражений (1.66) и (1.68) получим

(1.67)

т.е. мощность подобных насосов прямо пропорциональна плотности жид-кости, коэффициенту стеснения и КПД насоса в первой степени, диаметру колеса в пятой степени и частоте вращения в третьей степени.

В случае перекачки одной и той же жидкости модельным и натурным насосом 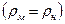, а также в первом приближении принимая ; ; 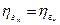; 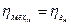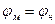формулы пересчета (1.65) – (1.67) упращаются и представляются в более удобном для решения практических задач виде:

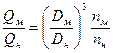; (1.68)

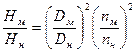; (1.69)

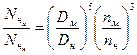(1.70)

Формулы (1.68) – (1.70) отражают законы подобия лопастных насосов.

Применив эти формулы пересчета для одного и того же насоса, пере-качивающего одну и ту же жидкость, получим закон пропорциональности (см. раздел 1.12).