Занятие №31. Криволинейный интеграл
№1. Вычислить криволинейные интегралы:
а)
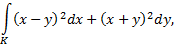
если  ломаная
ломаная 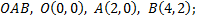
б)
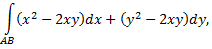
если  дуга параболы
дуга параболы 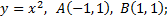
в)
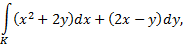
если  ломаная
ломаная 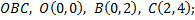
г)
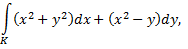
если  отрезок прямой от точки
отрезок прямой от точки 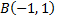 до точки
до точки 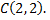
Примечание: криволинейный интеграл по длине дуги преобразуют к определенному интегралу. Записывают уравнение линии интегрирования (уравнение прямой или кривой) и преобразуют криволинейный интеграл в определенный интеграл с переменной  и вычисляют его. То есть, записывают чему равен
и вычисляют его. То есть, записывают чему равен 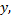 затем
затем 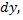 определяют пределы изменения переменной
определяют пределы изменения переменной 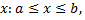 подставляют в криволинейный интеграл и решают его как обычный определенный интеграл относительно переменной
подставляют в криволинейный интеграл и решают его как обычный определенный интеграл относительно переменной 
Криволинейный интеграл по ломаной вычисляют как сумму интегралов, взятых по отрезкам разбиения.
№2. Применяя формулу Грина, вычислить
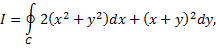
если 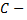 контур треугольника с вершинами
контур треугольника с вершинами 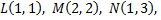 пробегаемый против хода часовой стрелки.
пробегаемый против хода часовой стрелки.
Примечание: если 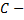 граница области
граница области 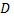 и функции
и функции 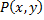 и
и 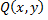 вместе со своими частными производными непрерывны в замкнутой области
вместе со своими частными производными непрерывны в замкнутой области 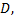 включая границу
включая границу 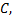 то справедлива формула Грина
то справедлива формула Грина
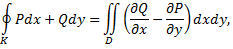
обход контура  выбирается так, что область
выбирается так, что область  остается слева.
остается слева.
В данном случае 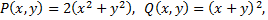 таким образом
таким образом
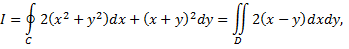
где область 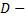 треугольник
треугольник 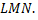 Уравнение прямой
Уравнение прямой  уравнение
уравнение 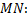
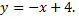 Вычисляют двойной интеграл по данной области
Вычисляют двойной интеграл по данной области
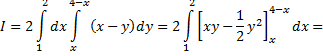

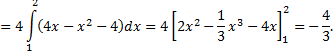
Теперь следует вычислить криволинейный интеграл по контуру, состоящему из звеньев 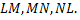
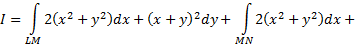
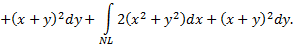
Уравнение 
Уравнение 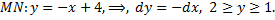
Уравнение 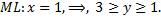
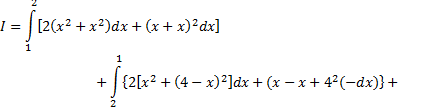
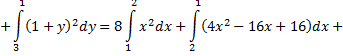

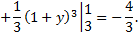
Дата добавления: 2015-08-11; просмотров: 1189;
