Занятие №27. Механические приложения определенного интеграла

№1. Материальная точка 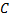движется прямолинейно со скоростью 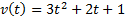м/с. Найти путь, пройденный точкой за промежуток времени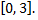

Примечание: если задана функция, определяющая скорость движения материальной точки по некоторой прямой, то путь, пройденный ее за некоторый промежуток времени определяется по формуле

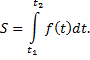
№2. Вычислить работу, которую нужно затратить, чтобы растянуть пружину на 10 см, если известно, что для удлинения ее на 1 см необходимо приложить силу в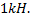

Примечание: работа силы, под действием которой движется материальная точка, определяется формулой

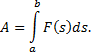
Пружина растягивается согласно закону Гука в нашем случае

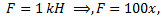т.е.

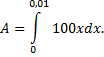
№3. Вычислить работу, которую необходимо затратить на выкачивание воды из резервуара 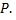Удельный вес воды принять равным Если 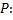правильная четырехугольная пирамида со стороной основания два метра и высотой пять метров.

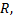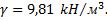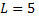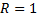№4. Определить работу, которую необходимо затратить на выкачивание воды из резервуара, представляющего собой лежащий на боку круговой цилиндр длиной и радиусом основания через находящееся вверху отверстие. Удельный вес воды Вычислить работу в случае, когда м, м.

Примечание: на высоте 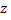выделим слой воды 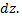Его объем

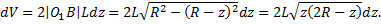
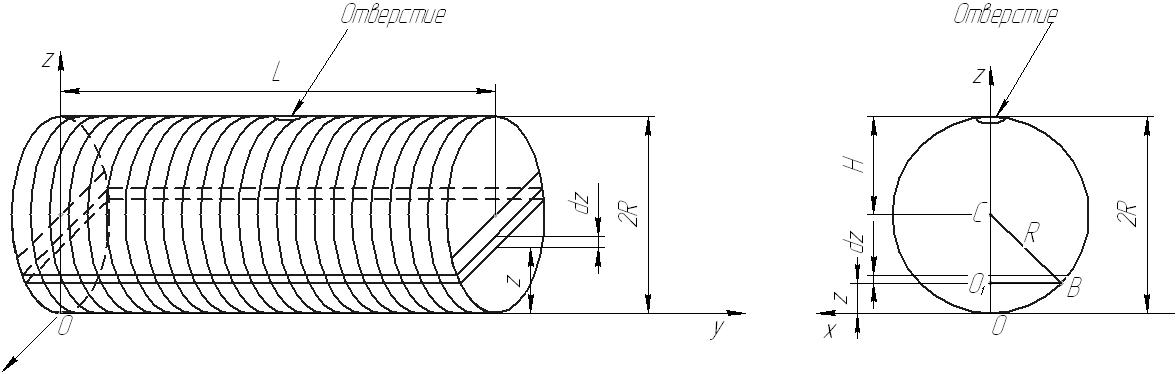
Рис. 72

Этот слой можно поднять на высоту 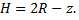Элементарная работа затраченая на выкачивание слоя 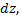определяется формулой

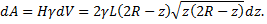
Работа по выкачиванию всей воды равна сумме всех элементарных работ

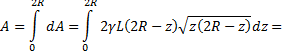
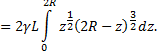
Теперь вычислим интеграл, который представляет собой интеграл от дифференциального бинома при Так как

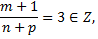
то для вычисления воспользуемся подстановкой

Имеем

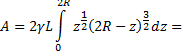
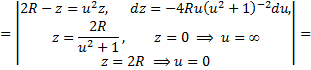
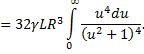
Подынтегральная функция в несобственном интеграле является правильной рациональной дробью, которую можно разложить в сумму простейших дробей. Интегралы от этих дробей

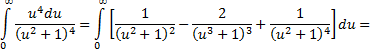
Таким образом,