Занятие №19. Экстремум функции двух переменных
№1. Исследовать на экстремум следующие функции
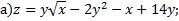
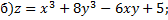
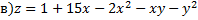 ;
;
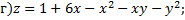
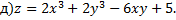
Примечание: если точка 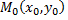 является точкой экстремума функции
является точкой экстремума функции 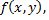 то
то 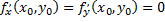 или хотя бы одна из этих производных не существует. Точки, для которых эти условия выполнены, называются стационарными. Пусть функция
или хотя бы одна из этих производных не существует. Точки, для которых эти условия выполнены, называются стационарными. Пусть функция 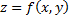 имеет непрерывные частные производные до третьего порядка включительно в некоторой области, содержащей стационарную точку
имеет непрерывные частные производные до третьего порядка включительно в некоторой области, содержащей стационарную точку 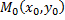 тогда:
тогда:
1) если 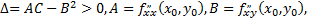
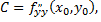 то точка
то точка 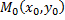 является точкой экстремума для данной функции, причем точкой максимума, если
является точкой экстремума для данной функции, причем точкой максимума, если 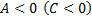 и точкой минимума при
и точкой минимума при 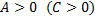 ;
;
2) если 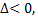 то в точке
то в точке 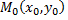 экстремума нет;
экстремума нет;
3) если 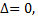 то экстремум может быть, а может и не быть.
то экстремум может быть, а может и не быть.
№2. Найти уравнение касательной плоскости и нормали к заданной поверхности 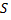 в точке
в точке 
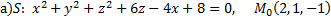
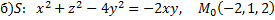
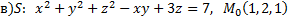
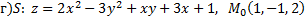
Примечание: если поверхность задана уравнением 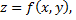 то уравнение касательной плоскости в точке
то уравнение касательной плоскости в точке 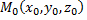 к данной поверхности
к данной поверхности
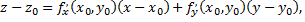
а каноническое уравнение нормали, проведенной через точку  поверхности
поверхности
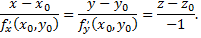
Когда уравнение поверхности задано в неявном виде 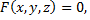 то уравнение касательной плоскости в точке
то уравнение касательной плоскости в точке  имеет вид
имеет вид
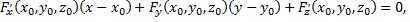
а уравнение нормали –
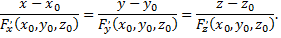
№3. Найти наибольшее и наименьшее значение функции 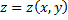 в области
в области 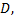 ограниченной заданными линиями:
ограниченной заданными линиями:
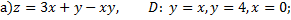

Дата добавления: 2015-08-11; просмотров: 794;
