Занятие №16. Дифференциал функции. Правило Лопиталя
№1. Найти дифференциалы функций

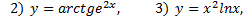
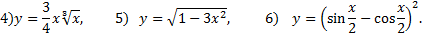
№2. Найти 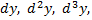 если
если 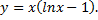
№3. Найти 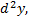 если
если 
№4. Сравнить приращение и дифференциал функции
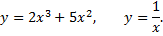
Примечание:
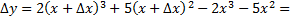
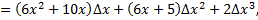

Разность между приращением 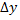 и дифференциалом
и дифференциалом 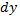 есть бесконечно малая высшего порядка по сравнению с
есть бесконечно малая высшего порядка по сравнению с 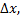 равная
равная 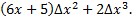
№5. Вычислить 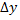 и
и  для функции
для функции 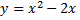 при
при 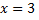 и
и 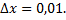
№6. Вычислить приближенное значение площади круга, радиус которого равен 3,02 м.
Примечание: воспользуемся формулой  Полагая
Полагая 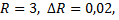 имеем
имеем

Следовательно, приближенное значение площади круга составляет
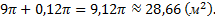
№7. Имеется металлический куб с ребром 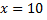 см. При нагревании ребро удлинилось на
см. При нагревании ребро удлинилось на  см. Насколько увеличился объем куба?
см. Насколько увеличился объем куба?
Примечание: объем куба 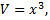 тогда
тогда 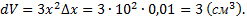 Увеличение объема
Увеличение объема 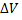 эквивалентно дифференциалу
эквивалентно дифференциалу 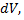 так что
так что 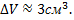 Полное вычисление дало бы
Полное вычисление дало бы 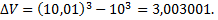 В этом результате все цифры, кроме первой, ненадежны, значит, следует округлить до
В этом результате все цифры, кроме первой, ненадежны, значит, следует округлить до 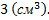
№8. Найти приближенное значение
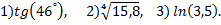
Примечание: 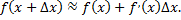
№9. Вычислить предел, используя правило Лопиталя
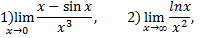
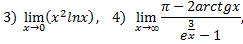
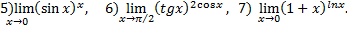
Примечание: Решая предел
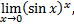
мы видим, что возникает неопределенность  Обозначим данную функцию через
Обозначим данную функцию через 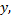 т.е.
т.е. 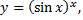 и прологарифмируем ее
и прологарифмируем ее
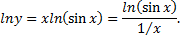
Вычислим предел логарифма данной функции, применяя правило Лопиталя
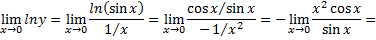
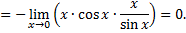
Следовательно,
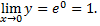
Примечание: Решая предел
 ,
,
мы видим, что возникает неопределенность 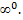 Положим
Положим 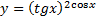 и прологарифмируем
и прологарифмируем
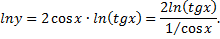
Применяя правило Лопиталя, получим

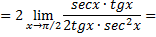
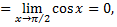
т.е.
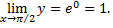
Примечание: Решая предел
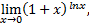
мы видим, что возникает неопределенность 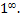 Логарифмируя и применяя правило Лопиталя, получим
Логарифмируя и применяя правило Лопиталя, получим
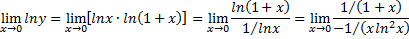
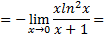
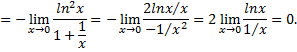
Таким образом,
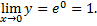
Дата добавления: 2015-08-11; просмотров: 1049;
