Доказательство. Пусть дана пара сил ( , ) с плечом АВ

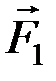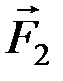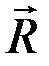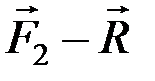Пусть дана пара сил ( , ) с плечом АВ. Разложим силу на составляющие и , тогда 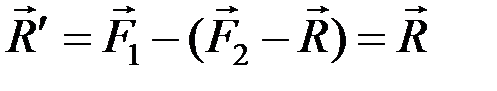, следовательно, имеем новую пару ( ).

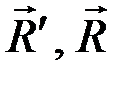На плече AC пара ( 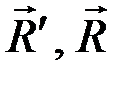) эквивалентна паре ( 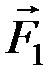, 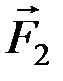), причем для любой пары плечо AC удовлетворяет условию 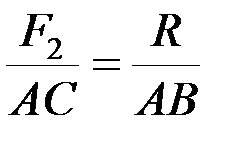или 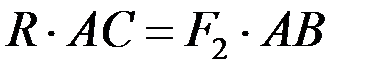. Теорема доказана.

Таким образом, задаваясь плечом, можно определить 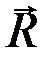, и наоборот.

Теорема.Две пары, лежащие в одной плоскости и имеющие равные моменты, статически эквивалентны.

Эту теорему доказывать не будем, т.к. она является следствием двух предыдущих теорем.

Совокупность пар называется системой пар.

Теорема.Система пар, расположенных в одной плоскости, эквивалентна одной паре с моментом, равным алгебраической сумме моментов слагаемых пар.

Доказательство. Возьмем две пары ( 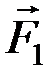, 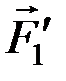) и ( 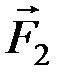, 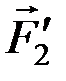), произвольно расположенные на плоскости. Приведем их к одинаковому плечу d. Согласно аксиоме А 3, силы 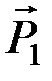, 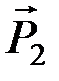и 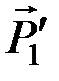, 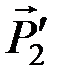можно алгебраически сложить: ; 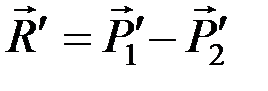. Силы 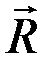и 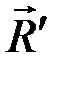равны по величине и противоположны по направлению, следовательно, это новая пара с моментом 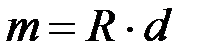, эквивалентным двум данным парам.

Нетрудно заметить, что 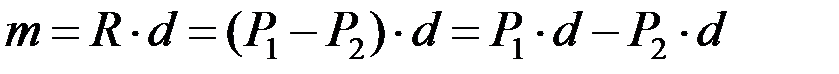. Это значит, что 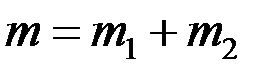или 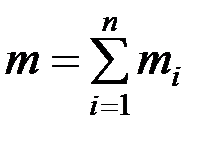(момент каждой пары должен быть взят со своим знаком).