Сложение двух параллельных сил, направленных в одну сторону
Теорема.Система двух параллельных сил, направленных в одну сторону, имеет равнодействующую, равную по величине их алгебраической сумме, параллельную им и направленную в ту же сторону. Линия действия равнодействующей проходит через точку, которая делит отрезок между точками приложения слагаемых сил на части, обратно пропорциональные этим силам внутренним образом.
Доказательство.Пусть на тело действуют две параллельные силы 
и 
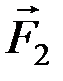. Соединим точки А и В отрезком прямой. Приложим к телу уравновешенную систему сил ( 
, 
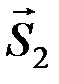) ~ 0 и найдем равнодействующие 
и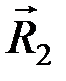 
. Перенесем 
и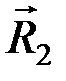 
в точку их пересечения О. Отметим, что ( 
, 
) ~ ( 
, 
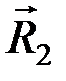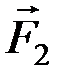). Разложим систему ( 
, 
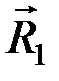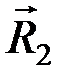) на составляющие ( 
, 
, 
, 
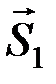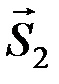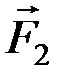). Т.к. ( 
, 
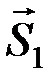) ~ 0, отбросим её. Силы 
и 
направлены параллельно друг другу. Согласно аксиоме А 3, их сумма равна 
. Переносим силу 
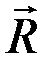вдоль ее линии действия в точку C на отрезке AB. Из подобия треугольников следует:
; 
.
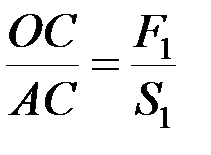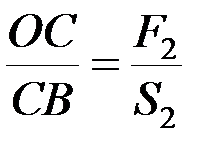
Разделив эти выражения друг на друга, получим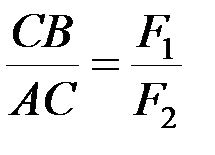 
или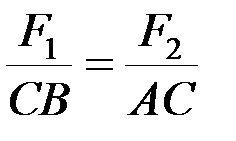 
.
Из свойств пропорции следует: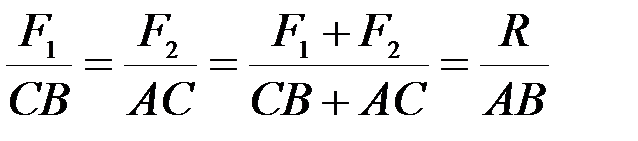 
, что и требовалось доказать.
Дата добавления: 2015-08-08; просмотров: 1003;