Пара сил и её свойства

Пусть имеются равные антипараллельные силы 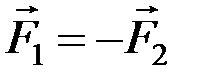, тогда 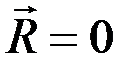; АС = ∞; ВС = ∞. Следовательно, точка С находится в бесконечности.

Система двух равных по величине параллельных и направленных в разные стороны сил называется парой сил (понятие ввел Франсуа Пуансо (1777 – 1859)).

Очевидно, что пара сил не имеет равнодействующей, следовательно, она не ведет к поступательному движению тела, а приводит тело во вращательное движение. Плоскость, в которой действует пара, называется плоскостью пары, расстояние между силами – плечом пары. Действие пары на тело зависит от величины сил, плеча и направления сил. Эта зависимость выражается в понятии момента.

Моментом пары называется вектор, величина которого равна взятому со знаком плюс или минус произведению одной из сил пары на плечо пары.

Будем считать: при знаке «+» момент направлен против часовой стрелки; при знаке «–» – по часовой стрелке. Размерность момента – Н·м.

Теорема.Не нарушая кинематического состояния тела, можно переносить пару в любое положение в плоскости её действия.

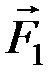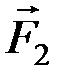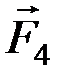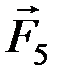Доказательство. Пусть на тело действует пара ( , ). Произвольно на таком же плече А₁В₁ возьмём две уравновешенные пары ( , ) и ( , ), эквивалентные нулю. Продлим их линии действия и сложим силы , , , .

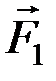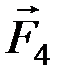Равнодействующие силы и равны по величине, направлены по одной линии (диагональ ромба) и противоположны. Остается система сил ( , 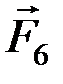), эквивалентная ( , 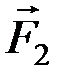). Т.к. точки A₁B₁ выбирались произвольно, теорема доказана.

Теорема.Не изменяя действия данной пары на тело, можно силу и плечо пары изменять любым способом, но так, чтобы момент пары остался неизменным.