Равновесие сходящейся системы сил

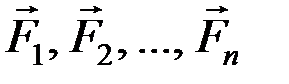Пусть имеется система сил ( ), линии действия которых пересекаются в одной точке. Такая система сил называется сходящейся.

Перенесем все силы вдоль линий их действия в точку О, т.е. заменим её другой системой сил, приложенных в точке О. Равнодействующая такой системы равна векторной сумме данных сил, и линия её действия проходит через точку О. Зная, что все силы можно заменить равнодействующей, можно сформировать условие равновесия твердого тела под действием такой системы сил, а именно: для того чтобы твердое тело, находящееся под действием сходящейся системы сил, было в равновесии, необходимо и достаточно, чтобы равнодействующая этих сил равнялась нулю:

.

Геометрическое условие состоит в том, что силовой многоугольник, построенный на слагаемых силах, должен быть замкнутым, т.к. геометрически равнодействующая изображается вектором, замыкающим силовой многоугольник.

Из равенства следует, что , если или

.

Для равновесия системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из трёх координатных осей равнялась нулю. Данное положение выражает аналитическое условие равновесия сходящейся системы сил.

Если все силы расположены в одной плоскости xOy, то достаточно двух уравнений в системе:

.

Задачи, в которых число неизвестных не превышает числа уравнений равновесия, называются статически определимыми; если число неизвестных превышает число уравнений – статически неопределимыми.

Например, для системы, изображенной на рисунке, можно составить только два уравнения равновесия, т.к. система сил плоская, а неизвестных – три (Т_А, Т_С и Т_В). Такая задача является статически неопределимой и решается с учетом деформаций в курсе «Сопротивление материалов».