Основы надежности машин.
3.1.1 Надежность и ее оценка.
Надежность - свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях использования, технического обслуживания, ремонта, хранения и транспортирования.
Надежность слагается из безотказности, ремонтопригодности, долговечности и сохраняемости изделия.
Под безотказностью понимают свойство изделия сохранять непрерывную работоспособность, под долговечностью - свойство изделия сохранять работоспособность до предельного состояния с необходимыми перерывами для технического обслуживания и ремонта; под ремонтопригодностью - свойство изделия, позволяющее производить его ремонт и техническое обслуживание, а под сохраняемостью понимают свойство изделия сохранять показатели качества в течение срока хранения и транспортирования, а также после них.
Долговечность - это свойство объекта сохранять работоспособность до определенного состояния (неустраняемого отказа) с необходимыми перерывами для технического обслуживания и ремонта.
Показатели безотказности различают для невосстанавливаемых и восстанавливаемых изделий. Для невосстанавливаемых изделий понятия безотказность, долговечность и надежность совпадают. Для восстанавливаемых изделий безотказность - это одно из свойств, определяющих их надежность. Показателями безотказности восстанавливаемых изделий являются вероятность безотказной работы, средняя наработка на отказ, интенсивность отказов; невосстанавливаемых изделий - вероятность безотказной/работы, наработка на отказ, характеристика и параметр потока отказов. Расчеты приведенных показателей проводятся на базе теории вероятностей.
Для определения показателей безотказности невосстанавливаемых изделий необходимо знать распределение отказов как случайных событий.
Распределение описывается характеристиками плотности распределения отказов f(x), интегральной функцией распределения отказов Q(x) и вероятностью безотказной работы Р(х). Первые две характеристики связаны зависимостью
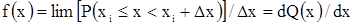 (3.1)
(3.1)
Отсюда произведение f(x)Δx при достаточно малом Δх приблизительно равно вероятности нахождения х в интервале 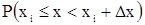
Дата добавления: 2015-08-08; просмотров: 968;
