Плотность распределения позволяет найти вероятность того, что

случайная величинах заключена между x₁ и х₂:

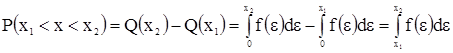(3.4)

Площадь распределения дает возможность найти среднюю наработку на отказ:

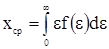
Интегральные функции Р(х) и Q(x) могут быть представлены графиками (Рисунок 65). По этим графикам можно определить вероятность безотказной работы и появления отказа, если известна наработка х.

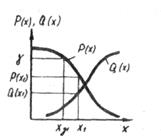
Рис 65. Рис 66.

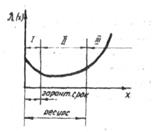
Условие отсутствия отказов до рассматриваемого момента времени может быть выражено интенсивностью отказов:

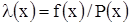(3.5)

На рисунке 66. приведен распространенный вид функции интенсивности отказов. Здесь наработка распределена на три периода. Период I относится к приработке изделия, когда интенсивность отказов повышена. Период II называется периодом нормальной эксплуатации, когда интенсивность отказов является минимальной и интенсивность отказов постоянна по величине. В периоде III начинают появляться отказы из-за интенсивности износа, усталостных разрушений, старения и других причин, обусловленных длительностью эксплуатации.

При испытаниях или наблюдениях в эксплуатации определяются (по известным методикам) приближенные значения показателей безотказной работы, но которым можно оценить точные их значения, полученные по вышеприведенным формулам.

Так, например, для приближенного определения безотказности надо знать и наработки до отказа или до конца испытаний: х₁,х₂,.... х_n.

Тогда вероятность появления отказа к наработке х_о, когда отказало N' изделий и сохранило работоспособность N' = N - N' изделий, составит

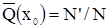(3.6)

Здесь и далее приближенные оценки будем обозначать теми же буквами, но с черточками сверху.