Термодинамике.

Тепловая машина. Второе начало термодинамики.

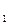Рассмотрим схему работы тепловой машины. Она состоит из термодинамической системы, называемой рабочим телом, которое сначала приводится в тепловой контакт с телом, температура которого больше температуры рабочего тела (нагреватель), а затем – с телом, температура которого меньше температуры рабочего тела (холодильник) От нагревателя рабочее тело получает количество тепла Q , а холодильнику отдает 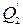и возвращается в исходное состояние (рис.1.14.1) Рис.1.14.1.

Поскольку изменение внутренней энергии за цикл равно

нулю то из (1.12.7) следует

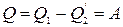. (1.14.1)

Отношение 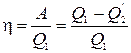(1.14.2)

называется коэффициентом полезного действия.

где Q= Q 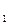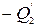— полное количество тепла, полученное двигателем, А— произведенная им работа.

Любой тепловой двигатель работает по замкнутому циклу, например, как на рис.(1.14.1). Если про­цесс совершается по часовой стрелке, то работа, производимая двигателем за цикл, А > 0.

Пусть Q₁ — поглощенное тепло, a Q’₂ — отдаваемое тепло (Q’₂ > 0). Опыт по­казывает, что тепло Q’₂ неизбежно существует в любом тепловом двигателе (как тепловой «шлак»), т.е. всегда h <1. Это соотношение выражает смысл второго начала термодинамики: невозможен круговой процесс, единственным результатом которого было бы производство работы за счет уменьшения внутренней энергии теплового резервуара (нагревателя).

Если бы не этот запрет, можно было легко решить энерге­тическую проблему — построить двигатель, который отнимал бы тепло из океанов и целиком превращал его в работу. Подоб­ный двигатель по своим практическим последствиям представ­лял бы вечный двигатель 2-го рода (в отличие от вечного дви­гателя 1-го рода). При современном по­треблении энергии человечеством температура океанов за 1000 лет уменьшилась бы не более чем на один градус Цельсия.

Существует другая формулировка второго начала термодинамики: теплота не может самопроизвольно переходить от тела, менее нагретого к телу более нагретому. Можно показать, что две приведенные формулировки эквивалентны.

Таким образом, работа, совершаемая системой в циклическом процессе всегда меньше, чем полученное ею количество тепла.

Поэтому второе начало термодинамики позволяет установить будет ли какой-либо процесс обратимым или необратимым. Если в некотором процессе 1-2 работа целиком переходит в тепло, то в обратном процессе 2-1 тепло должно полностью перейти в работу, чтобы процесс был обратимым. Это согласно второму началу термодинамики невозможно. Следовательно, такой процесс1-2 необратим.

Цикл Карно, теорема Карно. Термодинамическая шкала температур.

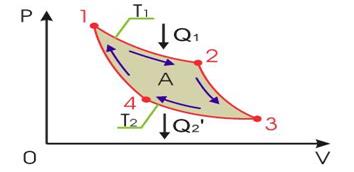
Рис.1.14.2.

Из различных круговых процессов особое значение в термодинамике имеет цикл Карно (рис.1.14.2). Это квазистатический идеальный процесс. Он заключается в следующем. Сначала систему приводят в тепловой контакт с нагревателем, имеющим температуру 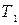. Затем бесконечно медленно уменьшая внешнее давление, ее заставляют квазистатически расширяться по изотерме 12. При этом она получает тепло от нагревателя и совершает работу 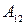. После этого систему адиабатически изолируют и заставляют квазистатически расширяться по адиабате 23, пока ее температура не достигнет температуры холодильника 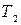. В этом процессе она также совершает работу 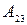и лтдает холодильнику тепло 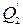. В состоянии 3 систему приводят в тепловой контакт с холодильником и изотермически сжимают до состояния 4. При этом система совершает отрицательную работу 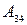(над системой работают внешние силы). Состояние 4 выбирается так, чтобы можно было квазистатическим сжатием по адиабате 41 вернуть систему в исходное состояние. В этом процессе система опять совершает отрицательную работу 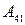. В результате за цикл система совершает работу 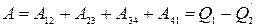. Рассчитав работу в каждом процессе, можно придти к теореме Карно: коэффициент полезного действия идеальной тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит от устройства машины и ее рабочего тела.

Термодинамическая шкала температур.

Из теоремы Карно следует

,

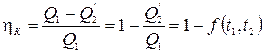где 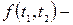универсальная функция выбранных эмпирических температур 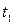и 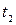. Тогда, как можно показать, введенную функцию можно заменить отношением некоторой функции , взятой при разных температурах,

.

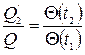Эту функцию , являющуюся однозначной функцией состояния называют абсолютной температурой. В дальнейшем будем обозначать ее Т.

Для определения численного значения абсолютной температуры используется шкала Кельвина. Она построена следующим образом. Принято, что температура тройной точки воды – это состояние, когда три фазы воды (лед, вода и водяной пар) находятся в равновесии, - равна 273,16К, а шаг этой шкалы равен шагу шкалы Цельсия. Поскольку температура тройной точки воды по шкале Цельсия равна 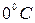, то температуру по шкале Кельвина можно найти .

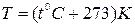Термодинамический смысл энтропии. Равенство Клаузиуса.

В термодинамике понятие энтропии было введено немецким физиком Р.Клаузиусом, который показал, что второе начало термодинамики может быть сформулировано строго математически, если ввести особую функцию состояния – энтропию. Он доказал, что для термодинамической системы, совершающей квазистатически циклический процесс, в котором система последовательно получает малые количества теплоты при соответствующих значениях температуры Т, интеграл от величины 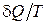по всему циклу равен нулю

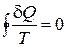. (1.14.3)

Это равенство называется равенством Клаузиуса. Оно эквивалентно второму началу термодинамики для квазистатических процессов. Из этого равенства следует, что можно ввести однозначную функцию состояния S, так чтобы ее полный дифференциал определялся

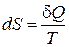. (1.14.4)

Эта функция называется энтропия. Заметим, что можно математически строго доказать, что эта функция эквивалентна понятию энтропия, введенному в статистической физике. Из (1.14.4) следует, что энтропию в термодинамике можно определить лишь с точностью до некоторой постоянной.

Неравенство Клаузиуса. Закон возрастания энтропии.

Из второго начала термодинамики можно сделать еще один вывод. Рассмотрим два равновесных состояния системы. Пусть переход из одного состояния в другое можно осуществить как с помощью квазистатического (обратимого) процесса, так и с помощью необратимого. Тогда можно показать, что количество тепла, полученное системой в обратимом процессе всегда больше, чем в необратимом. Отсюда следует:

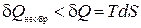и 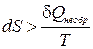. (1.14.5)

Таким образом, если адиабатически изолированная система переходит из состояния 1 в состояние 2 с помощью необратимого процесса 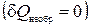, то

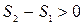, (1.14.6)

т.е. в таком процессе энтропия возрастает.

Для произвольного циклического необратимого процесса из (1.14.5) следует неравенство Клаузиуса

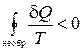. (1.14.7)

К.п.д. цикла Карно. Недостижимость абсолютного нуля температур.

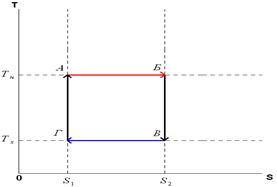
Рис.1.14.3.

Для расчета к.п.д. цикла Карно построим его график на диаграмме ТS (рис1.14.3). Процессы АБ и ВГ- изотермы, а БВ и ГА – адиабаты (в этом процессе энтропия постоянна). Работа, совершенная за цикл, определяется по площади фигуры, ограниченной линией графика. Количество тепла, полученного от нагревателя – по площади под линией АБ, которая изображает изотермический процесс контакта рабочего тела с нагревателем. Из (1.14.1) получим

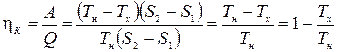. (1.14.8)

Из (1.14.8) следует вывод о недостижимости абсолютного нуля температур. Такой вывод является следствием теоремы Нернста. Опираясь на богатый экспериментальный материал, В.Нернст установил, что при 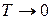энтропию системы нельзя изменить никакими воздействиями. Другими словами нулевая изотерма совпадает с адиабатой. Планк сузил теорему Нернста, наложив дополнительное условие. Он предположил, что при 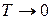и сама энтропия 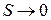: энтропия всякого тела стремится к нулю при стремлении к нулю температуры. Это утверждение носит название теоремы Нернста. Иначе его называют третьим началом термодинамики.

Из этой теоремы следует, что абсолютная температура не может быть равна нулю. Для доказательства рассмотрим цикл Карно и предположим, что холодильник имеет температуру равную нулю – процесс ВГ происходит при нулевой температуре. Согласно второму началу термодинамики

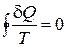или .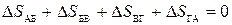

Но 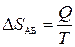, 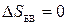(адиабатический процесс), 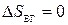(по теореме Нернста), 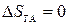(адиабатический процесс), следовательно, 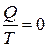, хотя 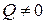. Это противоречие указывает, что нельзя достигнуть абсолютной температуры равной нулю.

Как уже отмечалось, энтропию в термодинамике можно определить с точностью до некоторой постоянной. Поэтому нужно выбрать нулевое значение, от которого ее можно отсчитывать. Это можно сделать, исходя из определения энтропии в статистической физике (1.11.20). При абсолютном нуле температуры система могла бы находиться в одном единственном состоянии: все частицы системы находились бы в покое и, следовательно, ее статистический вес Г = 1. Поэтому по формуле (1.11.20) получим, что при Т = 0 энтропия S = 0.