Тура и энтропия

Статистическая физика и термодинамика.

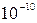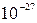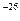Молекулярная физика представляет собой раздел физики, изучающий строение и свойства вещества, исходя из молекулярно-кинетических представлений. Согласно этим представлениям, любое тело состоит из огромного числа малых частиц – молекул. Размеры молекул имеют порядок м, а массы – порядка ( ÷ 10 )кг. Молекулы находятся в непрерывном, беспорядочном, хаотическом движении.

Существуют два взаимно дополняющих друг друга подхода к изучению свойств тел, обусловленных их молекулярным строением. Молекулярно-кинетическая теория истолковывает свойства тел как суммарный результат действия молекул. При этом она пользуется статистическим методом, интересуясь не движением отдельных молекул, а лишь средними величинами, которые характеризуют движение огромной совокупности частиц. Поэтому другое название этого метода – статистическая физика. Испольэуя этот метод, можно ввести конечное число величин, определяющих состояние системы – параметров (например, давление, концентрация частиц, температура и т.д.)

Второй метод – термодинамика. В отличие от молекулярно-кинетической теории термодинамика изучает макроскопические свойства тел, не интересуясь их микроскопическим строением и не вводя в рассмотрение молекулы. Для характеристики состояния системы она использует те же параметры, что и молекулярная физика. В основе термодинамики лежит несколько фундаментальных эмпирических законов (начал термодинамики), установленных на основании обобщения большой совокупности опытных фактов. В силу этого выводы термодинамики имеют весьма общий характер.

Вероятность и флуктуации. Статистические распределения.

Пусть имеется некоторая система, находящаяся в заданном состоянии, и какая- то характерная для системы величина х может иметь дискретные значения: 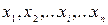. Проведем N измерений величины х. (Вместо того, чтобы производить повторные измерения над одной и той же системой, можно взять N одинаковых систем, находящихся в одном и том же состоянии, и по одному разу измерить величину х у всех этих систем. Такой набор одинаковых систем, находящихся в одинаковом состоянии, называется статистическим ансамблем.)

Допустим, что 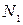измерений дали результат 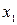, 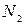измерений – результат 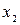…, 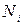измерений – результат 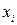и т.д. Величина

(1.11.1)

называется вероятностью появления результата .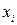

Если величина х может принимать непрерывный ряд значений (спектр х сплошной или непрерывный) то вероятность того, что при измерениях мы получим значение х, лежащее внутри интервала (х, х+dх), определится

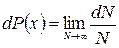, (1.11.2)

где dN - число измерений, результаты которых попали внутрь интервала dx. Очевидно, что эта вероятность будет пропорциональна ширине интервала dx, причем коэффициент пропорциональности будет зависеть от х. Тогда можно записать

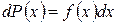. (1.11.3)

Функция 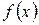называется плотностью вероятностей или функцией распределения вероятностей. Она подчиняется условию нормировки

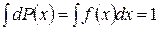, (1.11.4)

где интеграл берется по всем возможным значениям х.

Формулу (1.11.3) можно использовать для нахождения среднего по всем измерениям значения х или любой функции от х - :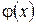

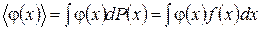. (1.11.5)

Флуктуации.

Вероятность случайного события и экспериментально наблюдаемая доля результатов, когда событие осуществляется, — это не одно и то же. Доля результатов испытывает случайные отклонения от предсказываемой вероятности. Именно такого рода отклонения происходят в любых макросистемах. Эти отклонения и обусловливают флуктуации.

Согласно теории вероятности, с увеличением числа N испытаний относительная флуктуация любой величины уменьшается по закону 1/ 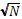. Именно грандиозность числа N молекул и объясняет, почему макроскопические законы, получаемые на основе статистических представлений о движении частиц макросистемы, оказываются точными.

В дальнейшем мы часто будем использовать понятие бесконечно малого объема dV макросистемы. Под этим будет пониматься такой объем, размеры которого ничтожны по сравнению с размерами самой макросистемы, но все же намного превосходящие характерный размер ее микростроения. Каждая бесконечно малая область содержит число частиц dN настолько большое, что относительной флуктуацией их можно пренебречь.

Распределение Гиббса.

Пусть система состоит из точечных частиц. Рассмотрим состояния, когда энергии частиц не выходят за пределы малого интервала (E, E+dE). Обозначим число таких состояний F(E) dE. Д.Гиббс сформулировал очень важный закон статистической физики: в состоянии теплового равновесия вероятность обнаружить любое состояние частиц макроскопического тела определяется только их полной энергией. Вероятность обнаружить состояние с полной энергией из интервала (Е, Е+dE) равна

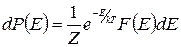. (1.11.6)

Это распределение вероятностей было названо распределением Гиббса. Здесь k - константа, называемая постоянной Больцмана, Т – абсолютная температура, Z - не зависящий от энергии коэффициент, называемый статистическим интегралом, величина которого определяется из условия нормировки (1.11.4)

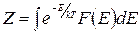. (1.11.7)

Интегрирование производится по всем возможным значениям энергии системы.

Таким образом, функция распределения Гиббса по энергиям имеет вид

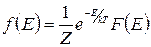. (1.11.8)

Распределение Максвелла по скоростям.

Из формулы (1.11.8) можно получить количественное описание распределения молекул по значению скорости для газа. Для этого будем полагать, что все молекулы имеют одинаковую потенциальную энергию, так что мы можем ее не учитывать. Кинетическая же энергия разных молекул различна. Тогда Е в (1.11.8) имеет смысл кинетической энергии молекулы. Проведя некоторые рассуждения, которые мы опускаем, можно получить

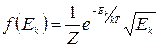, (1.11.9)

где .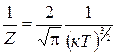

Если выразить кинетическую энергию молекулы 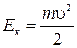, то получим функцию распределения молекул по модулю скоростей – функция распределения Максвелла:

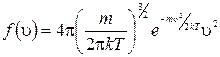. (1.11.10)

Зная эту функцию, можно найти количество молекул dN из общего числа N, скорости которых лежат в интервале от 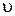до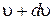

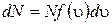. (1.11.11)

а) Рис.1.11.1. б)

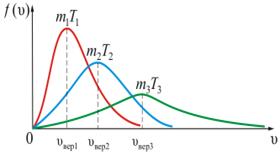
График этой функции распределения приведен на рис.1.11.1. Характерным для нее является то обстоятельство, что она имеет максимум, который характеризует наиболее вероятное значение скорости 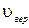или, другими словами, значение скорости, которым обладает наибольшее число молекул. Исследуя функцию (1.11.10) на максимум, получим значение этой наивероятнейшей скорости

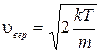. (1.11.12)

Эта скорость, как видно, зависит от температуры вещества и от массы молекулы.

Из рис.1.11.1а можно проследить за изменением f(υ) при изменении m и T. В данном случае 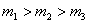(при T = const ) или 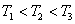(при m = const). Как следует из условия нормировки (1.11.4) площадь под кривой величина постоянная, равная единице, поэтому важно знать как будет изменяться положение максимума кривой:

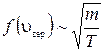кроме того .

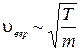Максвелловский закон распределения по скоростям и все вытекающие следствия справедливы только для газа в равновесной системе. Закон статистический, и выполняется тем лучше, чем больше число молекул.

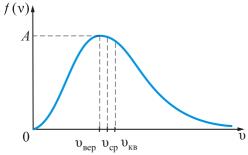
Используя определение среднего (1.11.5), найдем среднюю 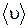и среднюю квадратичную 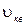скорости:

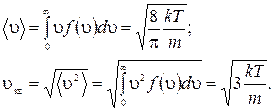(1.11.13)

Заметим, что 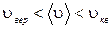(рис.1.11.1а).

Найдем теперь среднюю кинетическую энергию поступательного движения молекул 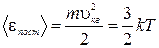. (1.11.14)

Мы пришли к важному выводу: абсолютная температура есть величина, пропорциональная средней энергии поступательного движения молекул.

Молекулы газа движутся хаотично и все направления их движения равновероятны. Поэтому средние квадраты проекций их скоростей на три взаимно перпендикулярных направления одинаковы 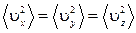. Кроме того 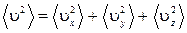. Тогда 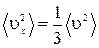. Поступательное движение характеризуется тремя степенями свободы и величина 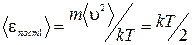определяет энергию, приходящуюся на одну степень свободы. Отсюда выводится закон равнораспределения классической физики: на каждую степень свободы молекулы приходится в среднем одинаковая кинетическая энергия, равная . Заметим, что это касается поступательных и вращательных степеней свободы, на одну колебательную степень свободы приходится энергия в два раза большая, т.е. kT.

Экспериментально закон распределения молекул по скоростям был подтвержден в опытах О.Штерна и В.Герлаха.

Распределение Больцмана по потенциальным энергиям.

Пусть газ находится во внешнем потенциальном поле, но его молекулы между собой не взаимодействуют. Чтобы не учитывать кинетическую энергию, будем рассматривать только молекулы, имеющие одинаковые кинетические энергии (одинаковые скорости). В этом случае в распределении Гиббса (1.11.8) Е имеет смысл потенциальной энергии 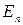и функция распределения – это распределение по координатам, поскольку от них зависит значение потенциальной энергии:

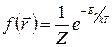, (1.11.15)

где Z также находится из условия нормировки (1.11.7): 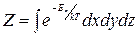, где интеграл берется по всем возможным значениям координат. Эта функция распределения носит название распределение Больцмана.

Рассмотрим для примера газ, находящийся в поле силы тяжести. Введем вертикальную координату z , направленную вверх. Тогда 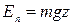и 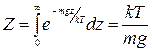. Отсюда функция распределения молекул по высоте

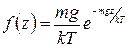. (1.11.16)

Найдем число частиц dN, находящихся в слое с координатами от z до z+dz (N - полное число частиц)

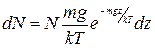(1.11.17)

Или концентрация (число частиц в единице объема) п на высоте z от некоторого нулевого уровня ( - концентрация при z=0)

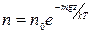. (1.11.18)

На рис.1.11.2 показаны два графика этого распределения, 1 и 2. График 2 соответствует более высокой температуре (по сравнению с графиком 1). Площадь под кривыми 1 и 2 на рисунке равна полному числу молекул в бесконечно высоком столбе, площадь которого равна единице. Отсюда следует, что площади под кривыми 1 и 2 одинаковы в данном случае.

Если газ представляет собой смесь разных газов, то в состоянии термодинамического равновесия концентрация n этих газов должна убывать с высотой экспоненциально с различной “скоростью” — в зависимости от масс молекул Рис.1.11.2.

Более крутая экспонента 1 на рисунке соответствует более тяжелым молекулам.