При любых процессах, протекающих в термодинамических изолированных системах, энтропия либо остается неизменной, либо увеличивается.

Таким образом, энтропия указывает направление самопроизвольно протекающих процессов. Рост энтропии указывает на приближение системы к состоянию термодинамического равновесия. В состоянии равновесия энтропия принимает максимальное значение. Закон возрастания энтропии можно принять в качестве еще одной формулировки второго закона термодинамики.

В 1878 году Л. Больцман дал вероятностную трактовку понятия энтропии. Он предложил рассматривать энтропию как меру статистического беспорядка в замкнутой термодинамической системе. Все самопроизвольно протекающие процессы в замкнутой системе, приближающие систему к состоянию равновесия и сопровождающиеся ростом энтропии, направлены в сторону увеличения вероятности состояния.

Всякое состояние макроскопической системы, содержащей большое число частиц, может быть реализовано многими способами. Термодинамическая вероятность W состояния системы – эточисло способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние. По определению термодинамическая вероятность W >> 1.

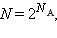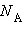Например, если в сосуде находится 1 моль газа, то возможно огромное число N способов размещения молекулы по двум половинкам сосуда: где – число Авогадро. Каждый из них является микросостоянием. Только одно из микросостояний соответствует случаю, когда все молекулы соберутся в одной половинке (например, правой) сосуда. Вероятность такого события практически равна нулю. Наибольшее число микросостояний соответствует равновесному состоянию, при котором молекулы равномерно распределены по всему объему. Поэтому равновесное состояние является наиболее вероятным. С другой стороны равновесное состояние является состоянием наибольшего беспорядка в термодинамической системе и состоянием с максимальной энтропией.

Согласно Больцману, энтропия S системы и термодинамическая вероятность W связаны между собой следующим образом:

где k = 1,38·10^–23 Дж/К – постоянная Больцмана. Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы.

Вероятностная трактовка второго закона термодинамики допускает самопроизвольное отклонение системы от состояния термодинамического равновесия. Такие отклонения называются флуктуациями. В системах, содержащих большое число частиц, значительные отклонения от состояния равновесия имеют чрезвычайно малую вероятность.