Физическая кинетика. Явления переноса.

Раздел термодинамики, изучающий процессы, возникающие при нарушении равновесия в термодинамических системах, называют физической кинетикой. Эти процессы являются необратимы.

Нарушение равновесия сопровождается возникновением потоков либо молекул, либо тепла, либо электрического заряда и т.п. Поэтому соответствующие процессы называют явлениями переноса.

Длина свободного пробега.

Медленность явлений переноса, например диффузии ароматических веществ – «распространение запаха», - при относительно высокой скорости теплового движения молекул (10³ м/с) объясняется столкновениями молекул. Молекула газа время от времени сталкивается с другими молекулами. В момент столкновения молекула резко изменяет величину и направление скорости своего движения. Расстояние, проходимое молекулой в среднем от одного столкновения до другого, называется средней длиной свободного пробега. Средняя длина свободного пробега равна: ,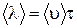

где 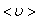– средняя скорость теплового движения, τ – среднее время между двумя столкновениями. Именно 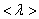- средняя длина свободного пробега нас интересует (рис. 1.17.1).

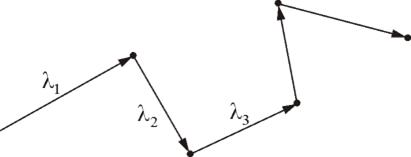
Рис. 1.17.1

Когда молекулы газа сближаются, силами взаимодействия между ними нельзя пренебречь. За счет этих сил молекулы могут сблизиться лишь на некоторое минимальное расстояние. Тогда молекулы можно представить как твёрдые шарики одного диаметра d, взаимодействующие между собой только при столкновении (рис.1.17.2). Обозначим σ –эффективное сечение молекулы, т.е. площадь, в которую не может проникнуть центр любой другой молекулы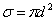

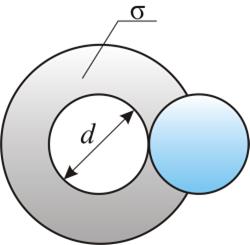
Рис. 1.17.2

За одну секунду молекула проходит путь, равный средней арифметической скорости 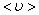. За ту же секунду молекула претерпевает ν столкновений. Следовательно, 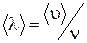(1.17.1)

Подсчитаем число столкновенийν.

Вероятность столкновения трех и более молекул бесконечно мала. Предположим, что все молекулы застыли, кроме одной. Её траектория будет представлять собой ломаную линию. Столкновения будут только с теми молекулами, центры которых лежат внутри цилиндра радиусом d (рис. 1.17.3).

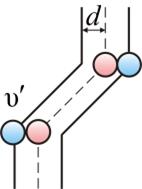
Рис. 1.17.3.

Путь, который пройдет молекула за одну секунду, равен длине цилиндра 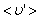. Умножим объём цилиндра 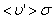на число молекул в единице объёма n, получим среднее число столкновений в одну секунду:

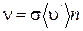. (1.17.2)

На самом деле, все молекулы движутся (и в сторону, и навстречу друг другу), поэтому число соударений определяется средней скоростью движения молекул относительно друг друга. По закону сложения случайных величин

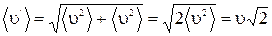. (1.17.3)

Тогда из (1.17.1) получим 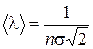(1.17.4)

Описание явлений переноса

Раздел термодинамики, изучающий процессы, возникающие при нарушении равновесия в системах, называется физической кинетикой. Такие процессы являются необратимыми. Нарушение равновесия сопровождается возникновением потоков либо молекул, либо тепла, либо электрического заряда и т.п. В связи с этим соответствующие процессы носят название явлений переноса. Каждое явление переноса бывает обусловлено неодинаковостью в пространстве значений некоторой величины.

При рассмотрении явлений переноса приходится вычислять количества различных величин (числа частиц, массы, энергии, импульса), переносимых через некоторую воображаемую поверхность. Количество какой – либо величины, проходящее в единицу времени через некоторую поверхность, называется потоком этой величины J. Поток является скалярной алгебраической величиной, знак которой зависит от выбора положительного направления. Кроме того, вводится понятие плотности потока. Это вектор, модуль которого равен потоку, проходящему через единичную поверхность, перпендикулярную направлению переноса j.

Процессы переноса в газах могут быть описаны с использованием молекулярно – кинетической теории. Будем считать, что молекулы газа совершают хаотическое тепловое движение. В этом случае можно полагать, что вероятность движения молекулы в любом направлении одинакова. Так как таких направлений шесть, то число молекул, движущихся в одном направлении, составляет 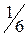от всего числа и плотность потока частиц в любом из этих направлений можно определить 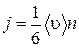, (1.17.5) где средний модуль скорости теплового движения молекул, п - концентрация молекул.

Рассмотрим перенос некоторой физической величины. Обозначим количество этой величины, приходящееся на одну молекулу 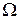(в качестве переносимой величины может выступать масса, импульс, энергия и т.д.). Будем считать, что эта величина изменяется в зависимости от координаты х как показано на рис.1.17.4.

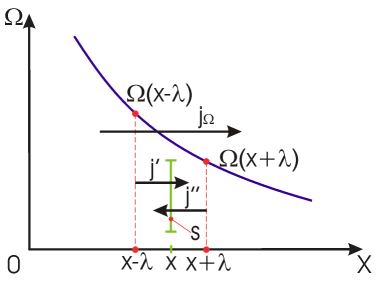
Рис.1.17.4.

Обозначим плотность потока молекул через сечение S в направлении оси х j’ , а в обратном направлении – j”. Каждая молекула переносит с собой величину 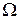. До рассматриваемого сечения смогут дойти молекулы, отстоящие от него не более, чем на длину свободного пробега 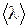. Поэтому значение величины 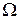, переносимое молекулами движущимися вдоль оси х равно 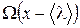, а в обратном направлении - 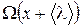. Тогда плотность потока величины 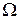через выбранное сечение будет определяться

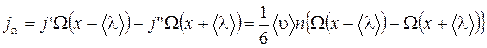. (1.17.6)

Полагая длину свободного пробега малой величиной, можно записать

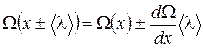. (1.17.7)

Подставляя эти выражения в (1.17.6), получим

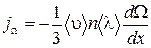. (1.17.8)

Стоящие в выражении (1.17.8) величины средней скорости 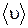, концентрации молекул п и переносимой физической величины 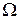зависят только от координаты х и в (1.17.8) принимают значения, соответствующие точке с координатой х.

Рассмотрим частные случаи.

Диффузия.

Диффузией называется обусловленное тепловым движением молекул самопроизвольное выравнивание концентраций в смеси двух или более различных веществ. Ограничимся рассмотрением только газообразных сред. Для простоты рассмотрим двухкомпонетную газовую смесь, в единице объема которой содержится молекул одного газа и 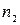молекул другого. Полное число молекул в единице объема равно 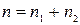. Чтобы упростить задачу, будем считать, что молекулы обоих газов мало отличаются по массе и имеют практически одинаковые эффективные сечения. В этом случае у них одинаковы средние скорости теплового движения, а в формуле для средней длины свободного пробега (1.17.4) стоит суммарная концентрация смеси.

Пусть диффундирующим газом будет первый и его концентрация зависит только от координаты х. В этом случае переносимую величину 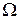можно представить 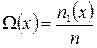. (1.17.9) Подстановка этого выражения в (1.17.8) дает уравнение диффузии в виде

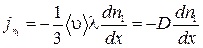, (1.17.10)

где введен коэффициент диффузии.

Аналогичные выражения могут быть записаны и для второго газа.

Теплопроводность газов.

Если температура в разных частях системы различна, то и средняя энергия молекул также будет различна. Перемещаясь вследствие теплового движения из одних мест в другие, молекулы переносят эту энергию, что и обуславливает процесс теплопроводности.

В данном случае переносимой величиной является средняя энергия теплового движения молекул. Полагаем, что температура зависит только от координаты х. Тогда 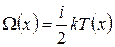, (1.17.11) где i - число степеней свободы молекулы. Подстановка этой величины в (1.17.8) дает 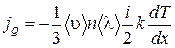. (1.17.12) Проведем ряд преобразований 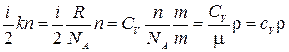, где R - универсальная газовая постоянная, 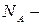число Авогадро, 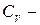молярная теплоемкость при постоянном объеме, 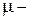молярная масса, 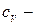удельная теплоемкость при постоянном объеме, 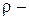плотность. Тогда уравнение теплопроводности запишется 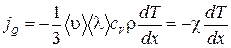, (1.17.13) где введен коэффициент теплопроводности 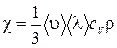. (1.17.14)

Внутреннее трение (вязкость) газов.

Пусть существует поток (направленное движение) молекул газа. Рассмотрим два соприкасающихся слоя газа небольшой толщины. Предположим, что слои движутся с различными скоростями. Каждая молекула газа участвует в двух движениях: хаотическом тепловом со средней скоростью 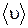и направленном со скоростью u , причем 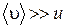. Попав из одного слоя в другой за счет хаотического движения, молекула соударяется с молекулами этого слоя, в результате чего ее импульс изменяется. В итоге импульс более быстро движущегося слоя убывает, а более медленного – возрастает. Таким образом, слои ведут себя так, как если бы между ними существовала сила трения, что обусловлено переносом импульса молекул.

Пусть направленное движение молекул происходит перпендикулярно оси х, а модуль скорости направленного движения зависит только от этой координаты 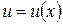. Роль переносимой величины играет в данном случае импульс молекулы 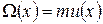. (1.17.14)

Подставляя (1.17.14) в (1.17.8), получим для плотности потока импульса, определяющего вязкость 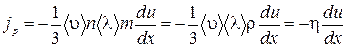, (1.17.15) где введен коэффициент вязкости 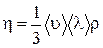. (1.17.16)

Как видно из приведенных соотношений между коэффициентами диффузии, теплопроводности и вязкости существует связь 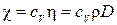. Кроме того отметим, что все указанные коэффициенты зависят от средней скорости теплового движения молекул, а, следовательно, от температуры.