Начало термодинамики.

Мы будем изучать раздел термодинамики, который занимается изучением закономерностей теплового движения в равновесных системах и при переходе систем в равновесие.

В термодинамике состояние системы характеризуется макроскопическими параметрами. К их числу относятся такие, например, как плотность, объем, концентрация частиц, внутренняя энергия, энтропия и т.д. (Заметим, что эти параметры можно истолковать и с точки зрения молекулярной физики.) Состояние системы называется стационарным, если характеризующие ее параметры не изменяются с течением времени. Если, кроме того, в системе нет и никаких стационарных потоков за счет действия внешних сил, то состояние называется равновесным. Система, не обменивающаяся энергией с внешними телами, называется термодинамически изолираванной.

Все параметры можно разделить на внешние и внутренние. Величины, определяемые положением не входящих в нашу систему внешних тел, называются внешними параметрами. Например, объем системы является ее внешним параметром, так как он определяется расположением внешних тел. Величины же, которые определяются совокупным движением и распределением в пространстве входящих в систему частиц, называются внутренними параметрами. Отметим, что при описании состояния системы существует один особый параметр, характеризующий состояние ее внутреннего движения и имеющий одно и то же значение для всех частей равновесной системы. Значения этого параметра для двух систем при их тепловом контакте обязательно становятся одинаковыми. Этот параметр называется температура. Исходными положениями термодинамики являются два основных постулата.

1. Первый постулат: изолированная система с течением времени всегда приходит в состояние термодинамического равновесия и никогда самопроизвольно выйти из него не может.

2. Второй постулат: все равновесные внутренние параметры являются функциями внешних параметров и температуры. Это утверждение может быть записано в виде уравнения, которое называется уравнением состояния

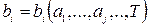(1.12.1)

Здесь 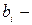некоторый внутренний параметр, 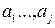- внешние параметры, Т – температура. В частности, в дальнейшем будем рассматривать простые системы. Простыми называются системы, состояния которых характеризуются одним внешним параметром, например объемом (V). Тогда, если внутренним параметром будет давление (р), то уравнение состояния имеет вид

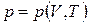(1.12.2)

Если систему вывести из состояния равновесия и затем предоставить самой себе, то через некоторое время она вернется в исходное состояние. Этот процесс перехода в исходное состояние называется релаксацией, а время перехода – временем релаксации.

Если в некотором процессе параметры системы меняются физически бесконечно медленно, т.е. время релаксации много больше времени, за которое изменяются параметры, то процесс называется равновесным или квазистатическим. Понятие квазистатического процесса является идеализацией. В природе нет таких реальных процессов.

Если происходит процесс, в котором система возвращается в исходное состояние и при этом не происходит никаких изменений в окружающих телах, процесс называется обратимым. Всякий квазистатический процесс является обратимым, но не каждый обратимый – квазистатическим.

Внутренняя энергия

Внутренней энергией U макросистемы называют величину, состоящую из:

1) суммарной кинетической энергии хаотического движения молекул в Ц-системе, связанной с самой системой (в этой системе отсчета суммарный импульс всех молекул равен нулю, и система как целое покоится);

2) собственной потенциальной энергии взаимодействия всех молекул, т.е. энергии взаимодействия только между молекулами, принадлежащими данной системе;

3) внутренней энергии самих молекул, атомов, ядер, …

Важным свойством внутренней энергии U является то, что она является функцией состояния и не зависит от того, каким путем мы привели систему в данное состояние. При изменении состояния приращение внутренней энергии определяется только конечным и начальным состояниями и не зависит от процесса, который перевел систему из одного состояния в другое.

Пока мы не будем включать во внутреннюю энергию U внутреннюю энергию молекул и атомов, считая во многих процессах вклад этой энергии в U постоянным, не зависящим от вида процесса. Т.е. будем считать, что U определена с точностью до некоторой постоянной.

Если макросистема состоит из нескольких частей, то энергией межмолекулярного взаимодействия на границах этих частей (в тонком слое) можно пренебречь и считать, что внутренняя энергия всей системы практически равна сумме внутренних энергий ее частей. Это значит, что внутренняя энергия является величиной аддитивной.

Внутренняя энергия является внутренним параметром системы и на основании второго постулата термодинамики можно написать

U=U(V,T) . (1.12.3)

Это уравнение называется калорическим уравнением состояния.

Работа в термодинамике и теплообмен

Внутреннюю энергию макросистемы можно изменить, совершив над системой работу A’ внешними макроскопическими силами, либо путем теплопередачи. При совершении работы изменяются внешние параметры, при теплообмене внешние параметры не меняются.

Совершение работы сопровождается перемещением внешних тел, действующих на систему (так например, ведет себя поршень в цилиндре с газом). Работу, совершенную простой системой при бесконечно малом изменении объема, можно рассчитать:

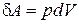. (1.12.4)

Работа при конечном изменении объема

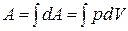. (1.12.5)

Отметим, что работа A существенным образом зависит от процесса (или “пути”), по которому система переводится из состояния 1 в 2. Это наглядно видно из графика (рис.1.12.1), где изображен процесс изменения объема на диаграмме p, V. Мы знаем, что геометрическая интерпретация интеграла (1.12.5)— это “площадь” под кривой 1-2, а эта площадь зависит от вида кривой, т. е. от процесса. Если в результате изменений Рис.1.12.1.

макросистема возвращается в исходное состояние, то говорят, что

она совершила круговой процесс или цикл. На диаграмме p, V такой процесс имеет вид замкнутой кривой. Работа, совершаемая системой за цикл, численно равна площади внутри цикла, тонированной на рис.1.12.2. При этом, если точка, изображающая состояние системы, описывает цикл по часовой стрелке (как на рисунке), то работа системы A > 0. Если же против часовой стрелки, Рис.1.12.2.

то A < 0.Знак работы зависит от знака dV: на тех участках процесса,

где dV > 0, работа A > 0, на тех же участках, где dV < 0, и A < 0.

Передача макросистеме тепла ‚ не связана с перемещением внешних тел. Она осуществляется путем непосредственной передачи внутренней энергии макросистеме от внешних тел при контакте с ними. Передача энергии при этом может происходить и через излучение. Энергия, переданная системе в результате теплообмена, называется количеством тепла. Величина 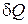тоже зависит от процесса. При этом, если 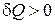, то система тепло получает, если же 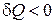, система тепло отдает.

Первое начало термодинамики

Первое начало термодинамики устанавливает, что внутренняя энергия системы является однозначной функцией состояния и изменяется только под влиянием внешних воздействий.

Математически это утверждение можно записать

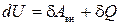, (1.12.6)

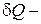где - работа внешних сил, количество тепла, полученное системой от внешних тел. Поскольку работа системы 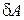и работа внешних сил 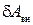равны по модулю и противоположны по знаку, (1.12.6) можно переписать

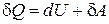. (1.12.7)

Из этого уравнения следует, что в случае, если процесс циклический (начальное и конечное состояния совпадают) изменение внутренней энергии равно нулю. Тогда система может совершить работу только за счет получения тепла от внешних тел 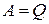. Поэтому первое начало термодинамики часто формулируют: невозможен вечный двигатель первого рода, т.е. такого периодического устройства, которое бы совершало работу, не заимствуя энергии извне.