Теплоемкость. Политропические процессы.
Теплоемкостью C тела называют количество тепла, которое нужно сообщить телу, чтобы повысить его температуру на один кельвин:
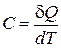 (1.13.1)
(1.13.1)
Эта величина, как и 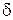 Q, зависит от процесса. Например, для процесса при постоянной температуре (изотермического)
Q, зависит от процесса. Например, для процесса при постоянной температуре (изотермического) 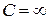 , а для адиабатного процесса, т.е. для процесса без теплообмена с окружающей средой, С=0. Без указания процесса выражение (1.13.1) не имеет смысла. Еще раз: теплоемкость C является функцией процесса.
, а для адиабатного процесса, т.е. для процесса без теплообмена с окружающей средой, С=0. Без указания процесса выражение (1.13.1) не имеет смысла. Еще раз: теплоемкость C является функцией процесса.
Мы будем пользоваться в основном молярной теплоемкостью C, теплоемкостью одного моля вещества, измеряемой в Дж/(моль К). В таблицах же обычно указывают удельную теплоемкость – теплоемкость единицы массы
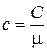 (1.13.2)
(1.13.2)
где c измеряется в Дж/(кг·К), 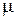 — молярная масса.
— молярная масса.
Так как 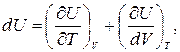 (1.13.3)
(1.13.3)
то, согласно (1.12.7) и (1.13.1) 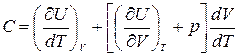 . (1.13.4)
. (1.13.4)
Такая форма записи подчеркивает, что при дифференцировании по T объем V следует считать постоянным, а при дифференцировании по V – постоянна температура.
Объем V зависит не только от температуры Т, но и от давления р. Поэтому в зависимости от процесса отношение  может принять любое значение и соответственно теплоемкость может принимать любое значение от
может принять любое значение и соответственно теплоемкость может принимать любое значение от 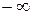 до
до 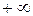 .
.
Особое значение имеют теплоемкости для двух процессов: теплоемкость при постоянном объеме СV, и при постоянном давлении Cp. Теплоемкость при постоянном объеме ( dV = 0) согласно (1.12.7) и (1.13.4) равна
 . (1.13.5)
. (1.13.5)
Опыт показывает, что во многих случаях теплоемкость C в широком интервале температур почти не меняется. Если считать, что C совсем не зависит от T, то из (1.13.5) следует:  , и можно написать простую формулу
, и можно написать простую формулу
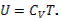 (1.13.6)
(1.13.6)
Произвольную постоянную интегрирования мы опустили, поскольку она не существенна: во все соотношения входит не сама функция U, а только разность ее значений (аналогично потенциальной энергии).
Если же в процессе остается постоянным давление, то
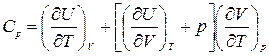 , (1.13.6)
, (1.13.6)
и  . (1.13.7)
. (1.13.7)
В термодинамике часто рассматривают процессы, в которых теплоемкость является величиной постоянной. Для такого процесса из (1.13.4), (1.13.5) и (1.13.7) следует
 ,
,
откуда  .
.
Тогда с учетом 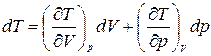 получим
получим
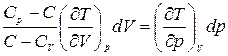 . (1.13.8)
. (1.13.8)
Это уравнение представляет собой уравнение политропического процесса в дифференциальной форме. Конкретные значения входящих в него частных производных зависят от самих систем, от их уравнений состояния. Принято вводить коэффициент, называемый показателем политропы
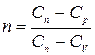 . (1.13.9)
. (1.13.9)
Здесь 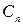 - теплоемкость в политропическом процессе.
- теплоемкость в политропическом процессе.
В частности, политропическими процессами являются изотермический, для которого n=1, и адиабатный - n = 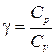 .
.
Дата добавления: 2015-08-08; просмотров: 874;
