Расчет работы в технической термодинамике.

В терминологии лекции 1 работа внешней среды над рабочим телом – это просто количество деформационного воздействия dw = pdv. Причем, ранее показано, что dw не является полным дифференциалом и что величина

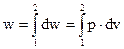(2.22)

сильно зависит не только от параметров начального и конечного состояния в точках 1 и 2 процесса, но и от его траектории.

Если известно уравнение связи p = p(v), то расчет количества работы сводится ко взятию интеграла в (2.22). В технической термодинамике эта связь давления и удельного объема чаще всего представляется в виде:

pvⁿ = const или pvⁿ = p₁v₁ⁿ, т.е. p = p₁v₁ⁿv^-n, при n = const. (2.23)

Это уравнение в технической термодинамике носит название политропы – каждое значение n определяет свою «тропу», т.е. траекторию, и отражает связи параметров p и v. Подробнее о политропах будем говорить в лекции 3.

Если подставить эту зависимость p = p(v) в (2.22), то получим табличный интеграл, который после несложных преобразований с помощью (2.23) приводится к одному из следующих видов:

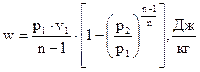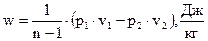или . (2.24)

Расчетные формулы (2.24) пригодны для политропического процесса для любого реального вещества.

Для идеального газа с учетом связи pv = R_уT расчетная формула в (2.24) несколько упрощается:

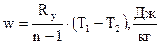(2.25)

Полная работа деформации (сжатия или расширения) за процесс рассчитывается как:

W = mw, Дж, где m – масса рабочего тела.

Если зависимость p = р(v) представлена в графическом виде,т.е. процесс с рабочим телом изображен на диаграмме p – v для какого-то вещества, то расчет количества работы можно провести в соответствии с рис. 2.4, как площадь под линией процесса до оси v.

Расчет количества работы возможен с помощью первого закона термодинамики:

Δu = q – w → w = q – Δu, (2.26)

если предварительно найти изменение внутренней энергии Δu и количество теплоты q так, как показано в этой лекции выше.

Замечание.В этом параграфе до сих пор шла речь о работе деформации рабочего тела, т.е. сжатия или расширения термодинамической системы в геометрическом пространстве. Однако, в технической термодинамике необходимо уметь рассчитывать работу проталкивания:

dw΄ = vdp, Дж/кг (2.27)

Особенно, этот расчет необходим для проектирования компрессоров и для определения мощности их привода. В этом случае (2.27) называют располагаемой работой.

На рис. 2.10 представлены две диаграммы в осях p – V теоретическая рабочая и p – v термодинамическая для процесса компремирования. Для идеального одноступенчатого компрессора этот процесс состоит из двух изобар и одной политропы с заданным показателем n.

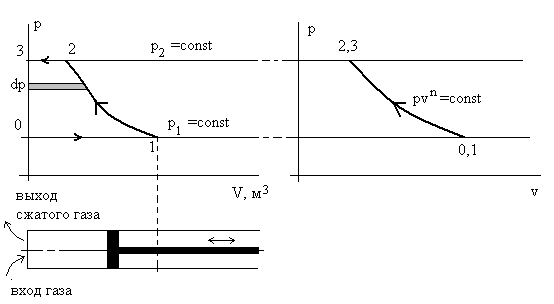
Рис. 2.10. Иллюстрация работы компрессора в диаграммах p – V и p – v.

Процесс 0 – 1 – всасывание исходной газовой среды, процесс 1 – 2 –

сжатие, 2 – 3 – проталкивание сжатого газа потребителю.

Площадь слева от кривой процесса сжатия pvⁿ = const и представляет собой затраченную на сжатие газа работу (располагаемая работа):

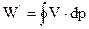. Дж.

Можно перейти к удельному объему v от геометрического V, если уделить последний на все количество газа m, вошедшего в цилиндр компрессора за весь процесс всасывания 0 – 1. Тогда техническая работа компрессора равна

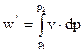Дж/кг. (2.28)

Снова воспользуемся уравнением политропы:

pvⁿ = const → pvⁿ = p₁v₁ⁿ → v = v₁p₁^1/n p^-1/n (2.29)

и подставим полученную зависимость v = v(p) в интеграл (2.28). Опять получается табличный интеграл, после преобразования результата интегрирования с помощью (2.29) окончательно приходим к равенству:

w΄ = nw, где w рассчитывается по (2.24) или (2.25).

Иными словами, работа, затраченная на компрессию газа (располагаемая) в n раз больше работы простого сжатия.

Мощность двигателя для привода одноступенчатого идеального компрессора рассчитывается как:

N_двиг = Gw΄/η, Вт, (2.30)

где G – массовый расход сжимаемого газа, кг/с, η – коэффициент полезного действия привода.

Замечание.В инженерной практике и, следовательно, в технической термодинамике приходится рассматривать процесс проталкивания газов через каналы, сопла (реактивные двигатели, газовые и паровые турбины). Линейные скорости течения газов в таких каналах настолько велики (звуковые и сверхзвуковые скорости), что процесс течения газа можно рассматривать как адиабатический (нет теплообмена). Это означает, что без учета трения потока газа о стенки канала и трения в самом потоке – s = const, ds = 0. В этой ситуации работа проталкивания рассчитывается через функцию состояния – энтальпию (2.5):

dh = Tds + vdp → dh = vdp → w΄ = 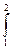dh = Δh = h₂ – h₁.

Здесь для идеального газа справедливо выражение (2.20), а для реального рабочего тела используются расчетные таблицы свойств веществ (например, «Таблицы состояния аммиака», «Таблицы для воды и водяного пара» и т.д.).