Внутренняя энергия идеального газа (свойства и расчет).

Из определения идеального газа следует, что внутренняя энергия (определение см. в лекции 1) идеального газа является просто кинетической энергией хаотического поступательного движения молекул газа. Потенциальная энергия взаимного расположения молекул в геометрическом пространстве, вращательная и колебательная энергия молекул идеального газа пренебрежимо малы по сравнению с кинетической энергией поступательного движения. Именно это обстоятельство позволило Больцману корректно провести усреднение кинетической энергии по множеству всех молекул и получить знаменитую формулу, известную из курса физики:

u = 3/2 kT, (2.18)

где k – постоянная Больцмана, Т – термодинамическая температура, u – средняя по множеству всех молекул кинетическая энергия.

Выражение (2.18) по существу показывает, что внутренняя энергия идеального газа является функцией толькотемпературы и что изменение внутренней энергии Δu определяется толькоизменением температуры:

(∂u/∂(∙))_T = 0

Здесь вместо точки в выражении частной производной можно подставить любой параметр состояния (конечно, кроме Т).

Отсюда сразу следует, что для идеального газа (см.(2.13) и (2.14)) расчет изменения внутренней энергии и энтальпии существенно упрощается, т.к. (∂u/∂v)_T = 0 и (∂h/∂p) = 0 и

du = c_vdT и dh = c_pdT → Δu = 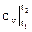(t₂ – t₁); Δh = 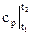(t₂ – t₁); (2.19)

И такой способ расчета изменений функций состояния справедлив для любых процессов с идеальным газом.

Можно также предложить другой способ расчета изменения функций состояния, если имеется в наличии диаграмма p – v или T – s для какого-то вещества в идеальном состоянии. Например, рассмотрим диаграмму T – s и процесс 1 – 2 на рис. 2.7.

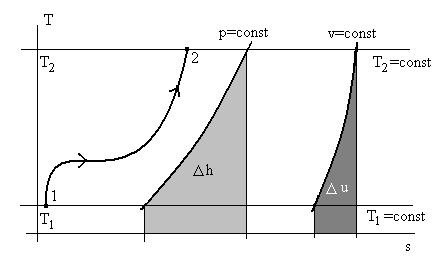
Рис 2.7. Графический способ расчета изменения

внутренней энергии и энтальпии для идеального газа в процессе 1 – 2.

Точки 1 и 2 характеризуют два состояния с температурами Т₁ и Т₂ (на рис 2.7 показаны две соответствующие изотермы). Изменение энтальпии Δh определяется (см.(2.5)):

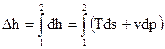, (2.20)

и для функций состояния Δh не зависит от траектории процесса, а зависит только от температуры в начальном и конечном состоянии (изотермы Т₁ и Т₂). Глядя на (2.20), видно, что по диаграмме T – s нельзя найти определенный интеграл от vdp. Тогда расчет Δh будем вести не по реальной кривой 1 -2 на рис 3.1, а по изобаре p = const (dp = 0 и vdp = 0) и второй интеграл станет нулевым.

Строим изобару p = const на диаграмме, тогда площадь под изобарой в нужном температурном интервале Т₁ и Т₂ и будет численно равна изменению энтальпии Δh.

Аналогично,

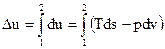(2.21)

Строим изохору v = const, и площадь под ней в тех же температурных пределах будет численно равна изменению внутренней энергии в процессе 1 – 2.

Замечание.Расположение изохоры или изобары на плоскости с координатами T – s правее или левее относительно процесса 1 – 2 здесь не существенно: площадь под кривыми неизменна.

Также просто найти изменение функций состояния в любомпроцессе с идеальным газом, если он изображен на диаграмме с координатами p – v. Предлагаем студентам самим проделать эту процедуру в качестве тренировки.

Замечание.Такая простота и легкость расчета изменения функций состояния в любом процессе обусловлена двумя обстоятельствами:

1. Зависимостью внутренней энергии идеального газа толькоот температуры.

2. Независимостью приращения функций состояния от траектории процесса, а, следовательно, возможностью выбора удобной для интегрирования траектории в интервале лишь температур начала и конца процесса.