Задачи к главе 9 для самостоятельного решения
9.1. Определить натяжение нити, связывающей два шарика объемом V=10см3 каждый, если верхний шарик плавает, наполовину погрузившись в воду. Нижний шарик в три раза тяжелее верхнего? Плотность воды ρ=1000 кг/м3.
Fнат=ρg V / 8.
9.2. Два шарика радиусами r1 и r2сделаны из материала плотностью ρ1 и ρ2 и соединены невесомым стержнем длиной l. Затем вся система помещена в жидкость плотностью ρ (ρ < ρ1 и ρ < ρ2). В какой точке стержня нужно прикрепить подвес, чтобы вся система находилась в равновесии при горизонтальном положении стержня?
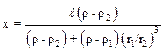 от шара плотностью r1.
от шара плотностью r1.
9.3. В сообщающиеся сосуды диаметрами D1и D2 налита вода. Как изменится уровень воды в сосудах, если положить кусок дерева массой m в первый сосуд? Во второй сосуд? Плотность воды r.
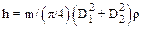 .
.
9.4. В сосуд с водой опущена длинная трубка сечением S = 2см2. В трубку налито m=72 г масла (ρм = 900 кг/м3 ).Плотность воды ρВ = 1000 кг/м3. Найти разность уровней масла и воды.
Δh = m (ρв - ρм ) / S ρв ρм .
9.5. При подъеме груза массой m = 2000 кг с помощью гидравлического пресса совершена работа А= 40 Дж. При этом малый поршень сделал n= 0 ходов, перемещаясь за один ход на h = 10 см. Во сколько раз площадь большого поршня больше площади малого?
S2/S1 = nhmg /A.
9.6. Из воды с глубины h1=7 м кран поднимает чугунную плиту массой m=1400 кг. Найти совершенную работу, если плита была поднята на высоту h2=5 м над водой. Плотность чугуна 7000 кг/м3. Считать g=10 м/с2. Плотность воды ρв известна.
А = mg[ h1(1- ρч /ρв) + h2 ].
9.7. Полый шар (внешний радиус R1, внутренний R2), сделанный из материала плотностью r1, плавает на поверхности жидкости плотностью r2. Какова должна быть плотность rвещества, которым следует заполнить внутреннюю полость шара, чтобы он находился в безразличном равновесии внутри жидкости?
r = [R13 (r2 - r1) + R23 r1] ( 1 / R23).
9.8. Один конец нити закреплен на дне, а второй прикреплен к пробковому поплавку. При этом 0,75 всего объема поплавка погружено в воду с плотностью ρв. Определить силу натяжения нити, если масса поплавка m= 2 кг и плотность пробки rп = 250 кг/м3 . Массой нити пренебречь.
T = mg (3ρв /4rп - 1).
9.9. Шарик всплывает с постоянной скоростью в жидкости, плотность которой в 4 раза больше плотности материала шарика. Определить силу сопротивления F жидкости при движении в ней шарика, считая ее постоянной. Масса шарика m=10 г.
F=3mg.
9.10. В цилиндрический сосуд налита ртуть и поверх ртути масло. Масса масла в 2 раза меньше массы ртути. Сосуд заполнен до высоты h=30 см. Определить давление на дно сосуда, если плотность ртути rр=1,36 ×104 кг/м3 , а плотность масла rм=900 кг/м3.
P=3rмrрgh/(rр+2rм).
9.11. С какой скоростью вытекает вода из узкого отверстия в дне бака, наполненного до высоты h=4,6 м? Вязкость не учитывать.
 .
.
Пример 10.1.
На космическом корабле-спутнике находятся часы, синхронизированные до полета с земными. Скорость V0 спутника составляет 7,9 км/с. На сколько отстанут часы на спутнике по измерениям земного наблюдателя по своим часам за время 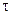 0=0,5 года.
0=0,5 года.
Dt-?
_____________________
V0=7,9 км/ч=7,9·103 м/с,
t0=0,5 года=15768000 с.
Решение.
Очевидно, что релятивистское замедление хода часов Dt=t-t0, где t – время в системе отсчета К’, движущейся вместе со спутником со скоростью V0 относительно "неподвижной" системы отсчета К, связанной с Землей. Так как (см. ) местное время t на спутнике равно
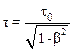 ,
,
то:
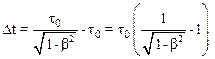 .
.
Для нахождения времени запаздывания Dt можно воспользоваться следующим приближением:
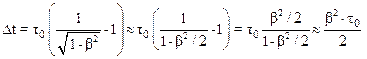 .
.
Подставляя численные значения, имеем:
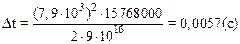 .
.
Пример 10.2.
Предположим, что мы можем измерить длину стержня с точностью 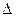 L=0,1 мкм. При какой относительной скорости U двух инерциальных систем отсчета можно было бы обнаружить релятивистское сокращение длины стержня, собственная длина L0 которого равна 1 м.
L=0,1 мкм. При какой относительной скорости U двух инерциальных систем отсчета можно было бы обнаружить релятивистское сокращение длины стержня, собственная длина L0 которого равна 1 м.
U-?
_______________
DL = 0,1 мкм=10–7 м,
L0 = 1 м.
Решение.
В соответствии с формулой (10.26) для Лоренцевского сокращения длины запишем:
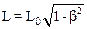 ,
,
где введено обозначение b=U/c.
Релятивистское сокращение длины можно было бы обнаружить при условии, что
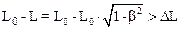 ,
,
или
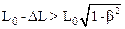 . (*)
. (*)
Разрешая соотношение (*) относительно b получим:
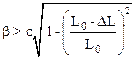 .
.
Проводя преобразования и опуская малую величину (DL)2 имеем для U выражение:
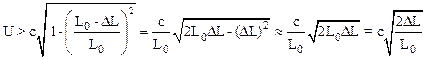 Подставляя численные значения, имеем:
Подставляя численные значения, имеем:
U=13,4·104 м/с.
Пример 10.3.
Ускоритель сообщил радиоактивному ядру скорость V1=0,4/с. В момент вылета из ускорителя ядро выбросило в направлении своего движения β-частицу со скоростью V2=0,75 с относительно ускорителя. Найти скорость U21 частицы относительно ядра.
U21 – ?
__________
V1=0,4 с,
V2=0,75 с
с=3×108 м/с.
Решение
Релятивистское сложение скоростей осуществляется по закону (10.30):
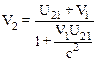 . (*)
. (*)
Из формулы (*) следует, что
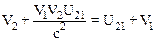 .
.
В результате последовательных преобразовании имеем:
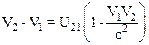
и
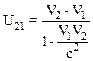 .
.
Подставив численные значения, получим
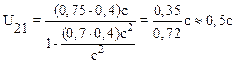 .
.
Дата добавления: 2015-08-08; просмотров: 3117;
