Задачи к главе семь для самостоятельного решения
7.1. Найти закон, по которому меняется натяжение F нити математического маятника, совершающего колебания по закону j=jmcoswt. Масса маятника m, длина – L.
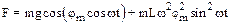
7.2. За 1 секунду амплитуда свободных колебаний уменьшается в два раза. В течение какого времени амплитуда уменьшится в 10 раз?
t=3,3 с.
7.3. Шар массой M=2,00 кг подвешен к двум соединенным последовательно пружинам. Коэффициенты эесткости пружин равны k1=1000 Н/м и k2=3000 Н/м. Пренебрегая массами пружин и трением найти: а) частоту малых колебаний шара, b) амплитуду колебаний, возникающих в случае, если шар установить на уровне, при котором пружины не напряжены, и отпустить без толчка.
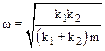 , А=26 мм.
, А=26 мм.
7.4. При неизменной вынуждающей силе амплитуда вынужденных колебаний при частотах w1=100 с–1 и w2=300 с–1 оказывается одинаковой. Найти резонансную частоту wРЕЗ.
wРЕЗ=224 с–1.
7.5. Шарик катается по дну сферической чашки. Предполагая, что эти колебания можно считать сунусоидальными, определить их период.
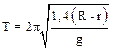
7.6. На каком расстоянии от центра нужно подвесить тонкий стержень длиной L, чтобы получить физический маятник, колеблющийся с максимальной частотой? Чему равна эта частота?
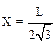 ,
, 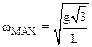 .
.
7.7. Однородный диск радиусом r совершает малые колебания относительно горизонтальной оси, перпендикулярной плоскости диска и проходящей на расстоянии а от его центра. Чему равен период колебаний диска?
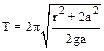
| 7.8. Блок (см. рис.) представляет собой сплошной цилиндр, который может вращаться вокруг своей оси без ощутимого трения. Масса блока М=5,0 кг, радиус R=10,0 см. Коэффициент жесткости пружины k=10 3 Н/м. Массой пружины и шнура можно пренебречь, проскальзывание шнура отсутствует. Масса груза m=1,0 кг. Определить частоту малых колебаний груза m. | 
|
w=16,9 с –1.
Пример 8.1.
Определить период колебаний математического маятника длиной L, точка подвеса которого опускается с ускорением w.
Решение
| T=? ____ L, g, w | 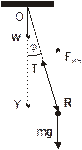
|
Запишем уравнение движения маятника в системе отсчета, связанной с ускоренно движущимся подвесом:
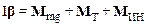 . (1)
. (1)
Проецируя уравнение (1) на вертикальную ось координат, имеем:
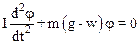 .
.
Решение этого уравнения аналогично решению уравнения (7.11) и имеет вид:
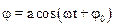 .
.
Циклическая частота колебаний маятника равна:
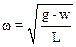 .
.
Полученный результат говорит о том, что под влиянием силы инерции происходит изменение периода колебаний математического маятника.
Пример 8.2.
Цилиндр массой m и радиусом R упирается в ступеньку высотой h. С каким наибольшим ускорением можно двигать подставку, чтобы цилиндр не перекатился через упор?
| a=? _____ m R h g | 
|
Решение
Цилиндр находится в покое относительно ускоренно движущегося основания. Отсутствию вращения относительно точки А соответствует равенство нулю результирующего вращательного момента сил, действующих на цилиндр. Выберем СО, жестко связанную с основанием и покажем силы, действующие на цилиндр: mg – сила тяжести, N – реакция горизонтального основания, Q –реакция ступеньки, ma – сила инерции.
При отсутствии вращения цилиндра относительно полюса О выполнено следующее условие:
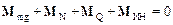 , (1)
, (1)
где момент силы Q равен нулю.
В проекции на ось Z уравнение (1) запишется так:
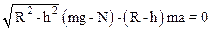 .
.
Выразим N:
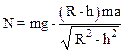 .
.
Вращение цилиндра не начнется, если N>0:
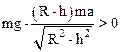 .
.
Из последнего соотношения следует, что
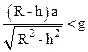 ,
,
или
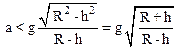 .
.
Дата добавления: 2015-08-08; просмотров: 2504;
