Задачи к главе 6 для самостоятельного решения

6.1. Три лодки одинаковой массы M движутся по инерции друг за другом с одинаковой скоростью v. Из средней лодки в крайние одновременно перебрасы­вают грузы массой m со скоростью u относительно лодок. Какие скорости будут иметь лодки после перебрасывания? Сопротивление воды не учитывать.

,V2 = V, .

6.2. Космический корабль должен, изменив курс, двигаться с прежним по модулю импульсом р под углом a к первоначальному направлению. На какое минимальное время должен быть включен двигатель с силой тяги F и как при этом нужно ориентировать ось двигателя?

t = 2p ·(sin a/2)/F, под углом b = (p + a)/2 к начальной скорости.

6.3. Космический корабль перед отделением последней ступени ракеты-носителя имел скорость v. После отбрасывания последней ступени его скорость стала равной 1,01v, при этом отделившаяся ступень удаляется относительно ко­рабля со скоростью 0,04v. Какова масса последней ступени, если масса корабля равна m0 ?

m = m0/3.

6.4. Граната, летевшая со скоростью 10 м/с, разорвалась на два осколка. Больший осколок, масса которого 60% массы всей гранаты, продолжал двигаться в прежнем направлении, но с увеличенной скоростью, равной 25 м/с. Найти скорость меньшего осколка.

v2 = 12,5 м/с.

6.5. Тело массой m соскальзывает с наклонной плоскости на неподвиж­ную платформу. Какую скорость будет иметь платформа, когда груз упадет на нее? Масса платформы M, высота начального положения тела h, угол наклона плоскости к горизонту a, коэффициент трения между наклонной плоскостью и телом k. Платформа движется без трения.

6.6. Плот массой М = 2000 кг находится на расстоянии s = 2 м от берега. Автомобиль массой m = 1000 кг перемещается от одного края плота к другому. Сможет ли при этом плот пристать к берегу, если длина плота L = 7 м.

Сможет.

6.7. На конце соломинки, лежащей на гладком столе, сидит кузнечик. С какой минимальной скоростью он должен прыгнуть, чтобы попасть на другой конец соломинки? Трение между столом и соломинкой не учитывать. Масса соломинки М, ее длина L, масса кузнечика m.

.

6.8. Снаряд массой m1 = 20 кг, летевший со скоростью v1 = 500 м/с под углом a = 30° к горизонту, попадает в платформу с песком массой m2 = 10 т и застревает в песке. Определите скорость движения платформы, если первона­чально платформа двигалась навстречу снаряду со скоростью v2 = 2 м/с.

v = 1,5 м/с.

6.9. Тело массой m = 1кг, брошенное с вышки в горизонтальном направлении со скоростью v₀ = 20м/с через t = 3с упало на землю. Определить кинетическую энергию Т, которую имело тело в момент удара о землю. Сопротивлением воздуха пренебречь.

= 633 Дж.

6.10. Насос выбрасывает струю воды диаметром d = 2 см со скоростью V = 20 м/с. Найти мощность N, необходимую для выбрасывания воды.

N=πρd²V³/8 = 1,26 кВт (ρ – плотность воды)

6.11. Какова мощность N воздушного потока сечением S = 0,55 м² при скорости воздуха V=20м/с и нормальных условиях?

N = ½ρSV³ = 2,84 кВт (ρ – плотность воздуха).

6.12. С какой наименьшей высоты h должен начать скатываться акробат на велосипеде (не работая ногами), чтобы поехать по дорожке, имеющей форму "мертвой петли" радиусом R = 4 м, и не оторваться от дорожки в верхней точке петли? Трением пренебречь.

h = 5R/2 = 10 м.

6.13. Конькобежец, стоя на льду, бросил вперед гирю массой m₁ = 5кг и вследствие отдачи покатился назад со скоростью V = 1м/c. Масса конькобежца m₂ = 60 кг. Определить работу А, совершенную конькобежцем при бросании гири.

390 Дж.

6.14. На рельсах стоит платформа, на которой закреплено орудие без противооткатного устройства так, что ствол его расположен в горизонтальном положении. Из орудия производят выстрел вдоль железнодорожного пути. Масса m₁ снаряда равна 10кг, и его скорость V₂ = 1км/с. На какое расстояние L откатится платформа после выстрела, если коэффициент сопротивления f = 0,002?

.

6.15. Со шкива диаметром d = 0.48 м через ремень передается мощность N = 9 кВт. Шкив вращается с частотой n = 240 мин^-1. Сила натяжения Т₁ ведущей ветви ремня в 2 раза больше силы натяжения Т₂ ведомой ветви. Найти силы натяжения обеих ветвей ремня.

Т₁ = 2N/(πnd) = 2,98 кН; Т₂ = N/(πnd) = 1,49 кН.

6.16. Кинетическая энергия Т вращающегося маховика равна 1 кДж. Под действием постоянного тормозящего момента маховик начал вращаться разно замедленно и, сделав N = 80 оборотов, остановился. Определить момент М силы торможения.

M = T/(2πN) = 1,99 H×м.

6.17. Тело массы m бросили под углом a с начальной скоростью V₀. Найти среднюю мощность, развиваемую силой тяжести за все время движения тела, и мгновенную мощность этой силы как функцию времени.

<Р> = 0, Р = mg(gt-V₀sinα).

6.18. В системе отсчета, вращающейся вокруг неподвижной оси с постоянной угловой скоростью w = 5,0 рад/с, движется небольшое тело массы m = 100 г. Какую работу совершила центробежная сила инерции при перемещении этого тела по произвольному пути из точки 1 в точку 2, которые расположены на расстояниях r₁ = 30 см и r₂ = 50 см от оси вращения?

А = ½mω²( 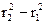) = 0,20 Дж.

6.19. Небольшая шайба массы m без начальной скорости соскальзывает с гладкой горки высотой h и попадает на доску массы M, лежащую у основания горки на гладкой горизонтальной плоскости. Вследствие трения между шайбой и доской шайба тормозится и, начиная с некоторого момента, движется вместе с доской как единое целое. Найти суммарную работу сил трения в этом процессе.

А = – μgh, где μ = mM/(m+M).

6.20. Парашютист массой m = 70 кг совершает затяжной прыжок и через t = 14 с имеет скорость V = 60 м/с. Считая движение парашютиста равноускоренным, найти работу по преодолению сопротивления воздуха.

.

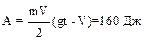6.21. Какую мощность должен развивать трактор при перемещении прицепа массой т = 5·10³ кг вверх по уклону со скоростью V = 1,0 м/с, если угол наклона α = 20°, а коэффициент трения прицепа μ = 0,20?

N = mgV(sinα+μcosα) = 26 кВт.

6.22. Пуля массой m ударяется о баллистический маятник массой М и застревает в нем. Какая доля кинетической энергии пули перейдет в теплоту?

.

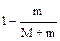6.23. Какая энергия пошла на деформацию двух столкнувшихся шаров массами m₁ = m₂ = 4,0 кг, если они двигались навстречу друг другу со скоростями V₁ = 3,0 м/с и V₂ = 8,0 м/с, а удар был прямой неупругий?

ΔЕ = m₁m₂(V₁+V₂)²/2(m₁+m₂) = 120 Дж.

6.24. Шар скатывается по наклонной плоскости с углом наклона a=30°. Какую скорость будет иметь центр шара относительно наклонной плоскости через 1,5 с, если его начальная скорость была равна нулю?

V = 5/7×(gtsinα) = 5,2 м/с.

6.25. Найти полезную мощность двигателя, приводящего в движение платформу в виде диска массой m₁ = 280 кг и радиусом R = 1,0 м, на краю которой стоит человек массой m₂ = 60 кг, если за t =30 с платформа приобретает скорость, соответствующую частоте n = 1,2 об/с.

.

6.26. Диск массой m₁ = 5 кг и радиусом R = 5 см, вращающийся с частотой n = 10 об/мин, приводится в сцепление с неподвижным диском массой m₂ = 10 кг такого же радиуса. Определить энергию, которая пойдет на нагревание дисков, если при их сцеплении скольжение отсутствует.

ΔΕ = 2π²n²R²m₁m₂/(m₁+m₂) =16 Дж.