Решение задач по динамике колебаний
Пример 7.1.
Маятник представляет собой невесомый стержень, на котором закреплены два небольших одинаковых груза – один на расстоянии L1 = 15 см, другой на расстоянии L2 = 30 см от точки подвеса. Определить период колебаний маятника.
T = ?
L1 = 15 см, L2 = 30 см
Решение.
Период колебаний физического маятника определяется формулой:
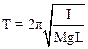, (1)
где M – масса маятника, I – его момент инерции, L – расстояние от точки подвеса до центра масс маятника. Выразим величины, определяющие величину периода.
|
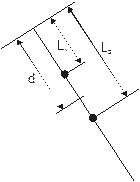
Пренебрегая массой стержня, получим, что M = 2m, момент инерции маятника, как аддитивная величина, равен:
.
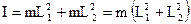Расстояние L найдем, используя определение центра масс:
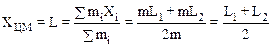. (2)
Подставляя найденные величины в (1), получим:
.
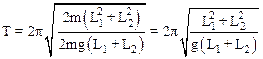Численные вычисления дают Т » 1 с.
Пример 7.2.
Пружинный маятник, колеблющийся в жидкой среде, в течение 50 секунд потерял 0,6 своей начальной энергии. Определить коэффициент сопротивления, если масса маятника 5 г.
r = ?
t = 50 c, m = 5 г = 5×10 –3 кг, DЕ = Е0 – Е = 0,6Е0, или E/E0 = 0,4
Решение.
Колебания маятника в жидкой среде (с трением) описываются уравнением:
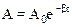, где b = r/m. (2)
Полная энергия маятника пропорциональна квадрату амплитуды:
,
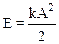здесь k – коэффициент жесткости пружины.
Зависимость полной энергии маятника от времени имеет вид:
.
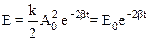По условию Е=0,4Е0. Тогда
.
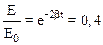Учитывая (2), имеем:
,
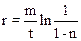откуда
r»9,16×10 –5 кг×с –1.
Пример 7.3.
Груз массой m = 10 кг, подвешенный к концу пружины, движется в жидкости. Коэффициент жесткости пружины с = 10 Н/см. Сила сопротивления движению R пропорциональна первой степени скорости груза: R = bV, где b = 1,6 H с/см. Найти закон движения груза, если в начальный момент груз был смещен из положения статического равновесия вниз на 4 см, и ему была сообщена вниз начальная скорость V0 = 4 см/с.
х = х(t)
FТР=rV, m=10 кг, k=10 Н/cм=10 3 Н/м, r=1,6 Н/см=1,6×103 Н/м,
х0=4 см=4×10–2 м, V0=4 cм/с=4×10–2 м/c.
Решение
|
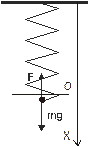
Движение груза описывается уравнением (7.22)
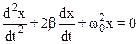, (1)
где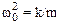 
, b=r/2m.
Подставив числовые значения, находим, что w0=10 рад/с, b=8 рад/с; таким образом, b<w, и в задаче рассматривается случай малого сопротивления (см. (7.4)).
Закон движения груза имеет вид:
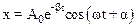, (2)
частота колебаний равна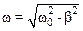 
.
Для определения постоянных А0 и a воспользуемся начальными условиями:
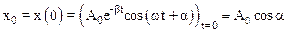, (3)
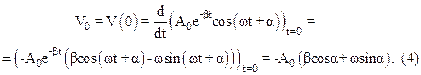Выразим из (3) А0 и подставим в (4). Имеем:
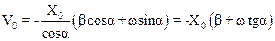(5)
Формула (5) позволяет получить выражение для a:
.
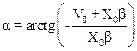Таким образом, искомое уравнение движения маятника имеет следующий вид:
.
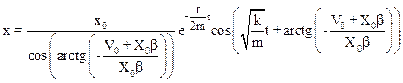Используя найденные ранее w0=10 рад/с, b=8 рад/с и начальные значения х0 и V0 находим: a=0,59 рад и w=6 рад/с.
Итак, груз совершает затухающие колебания по закону:
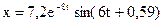×10–2 м. (6)
Дата добавления: 2015-08-08; просмотров: 1073;