Задачи к главе 3 для самостоятельного решения
3.1. Однородный стержень длиной 1,0 м и массой 5,0 кг подвешен горизонтально на двух параллельных веревках одинаковой длины. К стержню прикреплен груз массой 10 кг на расстоянии 0,25 м от одного из его концов. Определить натяжения веревок. (49 Н; 98 Н)
3.2. Через блок, прикрепленный к динамометру, переброшен канатик. Один конец канатика закреплен так, что образует угол a=60 градусов с вертикалью (рис. 1) . К другому концу подвешен груз массой m=5,0 кг. Определить показания динамометра.
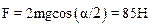
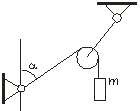 Рис. 1
Рис. 1
| 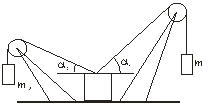 Рис.2
Рис.2
|
3.3. На горизонтальной плоскости лежит груз массой m=10 кг, к которому прикреплены веревки, перекинутые через блоки (рис. 2). К концам веревок подвешены грузы m1 и m2. Определить наибольшее значение массы груза m1, при котором система будет еще находиться в равновесии, если m2=5,0 кг, a1=45 градусов, a2=30 градусов, а коэффициент трения груза о горизонтальную плоскость m=0,50. Массами блоков и веревок и трением в блоках пренебречь.
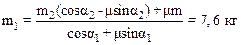
3.4. Однородный стержень массой m=2,0 кг подвешен на двух нитях одинаковой длины, равной a=50 см (рис. 3). Определить длину стержня, если натяжение нитей F=30 H.
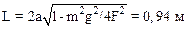
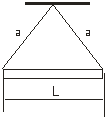 Рис.3 Рис.3
| 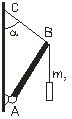 Рис.4 Рис.4
| 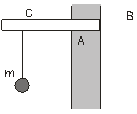 Рис.5 Рис.5
|
3.5. Стержень АВ массой m1=5,0 кг шарнирно прикреплен нижним концом к вертикальной стенке (рис. 4). К верхнему концу стержня, который привязан к стенке веревкой СВ, подвешен груз массой m2=3,0 кг. Определить натяжение веревки СВ, если ее длина в два раза меньше длины стержня АВ.
21 Н
3.6. На наклонной плоскости с углом наклона 35 градусов стоит однородный прямой цилиндр радиусом 10 см. Чему равна наибольшая высота цилиндра, при которой он еще не опрокинется?
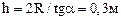
3.7. Однородная горизонтальная балка длиной 1,5 м и массой 50 кг закреплена в стене толщиной 50 см так, что опирается на нее в точках А и В (рис. 5). К свободному концу балки подвешен груз массой 100 кг. Определить силы реакций в опорах А и В.
FA=3,7 кН; FB=2,2 кН
3.8. Однородный шар массой 2 кг прикреплен к вертикальной стене с помощью нити (рис. 6). С какой силой шар давит на стену, если нить образует с ней угол a=30 градусов? Трение не учитывать.
F=FTtga=11 Н
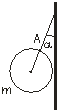 Рис.6
Рис.6
| 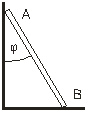 Рис. 7
Рис. 7
| 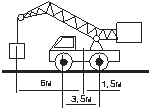 Рис. 8
Рис. 8
|
3.9. При каком наименьшем значении коэффициента трения между стеной и шаром (рис.6) точка А, в которой закреплена нить, и центр шара будут находиться на одной вертикали?
μ=1
3.10. Лестница АВ опирается концом А на вертикальную гладкую стену, а концом В- на пол (рис.7). Коэффициент трения лестницы о пол m=0,3. Чему равно наибольшее значение угла j, образованного лестницей с вертикальной стеной, при котором лестница будет еще находиться в равновесии?
tgφ=2μ; φ=31˚
3.11. На грузовом автомобиле установлен подъемный кран (рис.8). Масса автомобиля вместе с краном 3×103 кг. Расстояние между осями передних и задних колес 3,5 м. Какой максимальный груз может поднять этот кран, если задняя ось и точка, в которой подвешен груз, находятся на расстояниях 1,5 и 6 м от вертикальной плоскости, проходящей через масс автомобиля с краном?
1,5·103 кг
3.12. Найти координаты центра масс системы, состоящей из 4 шариков массами m2=200, m3=300, m4=400 и m1=100 г, которые расположены в вершинах и центре равностороннего треугольника со стороной 20 см. Координатные оси направить так, как указано на рисунке 9.
XC=0,12 м; YC=0,058 м
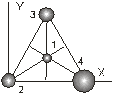 Рис.9 Рис.9
|  Рис.10
Рис.10
| 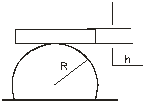 Рис.11 Рис.11
|
3.13. Определить положение центра масс стержня, состоящего из двух частей одинаковой длины и одинакового поперечного сечения, одна из которых свинцовая, а вторая железная, если его общая длина 0,50 м.
Центр масс смещен в сторону свинцовой части на
расстояние 0,25 м от геометрического центра стержня
3.14. В однородном диске диаметром 60 см вырезано круглое отверстие диаметром 20 см, центр которого находится на расстоянии 8,0 см от центра диска (рис.10). Определить положение центра масс диска.
Центр масс смещен на 0,01 м от центра диска
3.15. Брусок толщиной h лежит на неподвижном цилиндре, радиус которого R (рис.11). При каком соотношении между h и R брусок будет находиться в положении устойчивого равновесия? Считать, что трение между бруском и цилиндром достаточно велико.
h<2R
3.16. Масса колеса равна 100 кг, радиус 0,5 м. Какую минимальную силу можно приложить к колесу, чтобы перекатить его через балку высотой 0,10 м? При каком минимальном коэффициенте трения между колесом и выступом это можно сделать?
294 Н, mМИН=0,375.
3.17. Однородный стержень подвешен за концы на двух пружинах, у которых коэффициенты упругости равны k1 и k2. В нерастянутом состоянии длина пружин одинаковая, масса единицы длины стержня q. Под каким углом к горизонту будет висеть стержень при равновесии? Где нужно прикрепить вторую пружину, чтобы стержень висел горизонтально? Длина стержня ℓ.
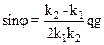 , на расстоянии
, на расстоянии 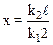 от середины стержня
от середины стержня
3.18. Под каким минимальным углом к горизонту нужно приложить силу к верхнему ребру прямоугольного ящика длиной l и высотой h, чтобы он перемещался, не переворачиваясь? Коэффициент трения равен f. Какова должна быть величина этой силы, если масса ящика равна m?
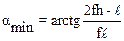 ,
, 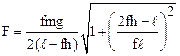
3.19. В открытый с обеих сторон полый цилиндр радиусом R, стоящий торцом на горизонтальной плоскости, положили два одинаковых шара радиусом r > R/2 и массой m. При какой минимальной массе М цилиндра шары его не опрокинут? Поверхности шаров и цилиндра считать гладкими, стенки цилиндра тонкими.
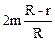
Пример 6.1.
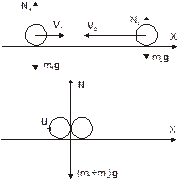
Два шарика массами m1 и m2 движутся навстречу друг другу по идеально гладкой поверхности со скоростями V1 и V2. Определите скорость U шариков после абсолютно неупругого удара.
U=?
m1, V1, m2, V2
Решение
На шарики действуют сила тяжести и сила реакции опоры, однако результирующаяих равна 0, т. е. можно применить закон сохранения импульса:
PІ= РІІ (1)
здесь PІ = p1 + р2 – импульс системы до взаимодействия (p1 = m1V1, p2 = m2V2), РІІ – импульс системы после взаимодействия, РІІ = (m1 + m2)U.
|
Выберем ось X вдоль направления движения первого шарика и запишем (1) в проекциях на ось X:
m1V1 - m2V2 = (m1 + m2)U,
откуда следует:
U=(m1V1- m2V2)/(m1+m2).
Пример 6.2.
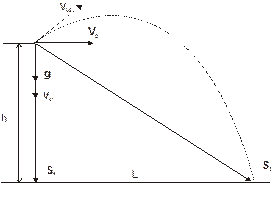
На высоте Н = 80 м снаряд, летящий горизонтально со скоростью V0 = 100м/с, разрывается на два равных осколка. Первый осколок через t1 = 2с падает в эпицентр взрыва. Определить дальность полета второго осколка L.
L=?
H=80 м, V0=100 м/c, t1=2c
Решение
Запишем уравнения кинематики для обоих осколков снаряда, учитывая (см. рис.) равнопеременный характер движения:
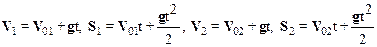 . (1)
. (1)
Эти уравнения в проекциях на оси координат имеют вид: 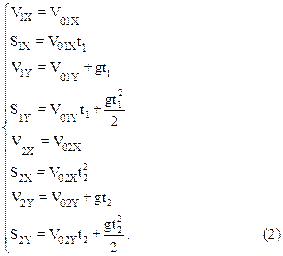
|
Из чертежа видно, что S1Y=S2Y=h, S2X=L. Поскольку первый осколок упал непосредственно под эпицентром взрыва, то S1X=V01Xt1=0. На этом основании можно записать, что V01X=0. С учетом сказанного перепишем систему (2) следующим образом:
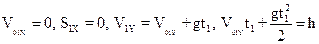
и
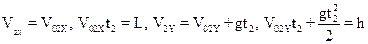 .
.
Из четвертого уравнения системы выразим скорость первого осколка после разрыва
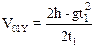 (4)
(4)
Из последнего уравнения системы (3) выразим время полета второго осколка t2:
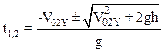 .
.
Заметим, что время полета не может быть отрицательным, поэтому условию задачи удовлетворяет только один корень:
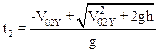 (5)
(5)
Подставив время t2 в шестое уравнение системы (3) найдем дальность L:
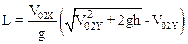 (6)
(6)
Для определения проекции скорости V02X воспользуемся законом сохранения импульса. Если рассматривать два состояния системы, в первом из которых система находится за мгновение до разрыва, а во втором – мгновение после разрыва, то при этом Dt®0 и импульс силы тяжести, действующий на систему мал, и ее импульс сохраняется. Можно записать:
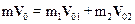 , (7)
, (7)
здесь m1=m2=m/2 – массы первого и второго осколков. Проецируя уравнение (7) на оси координат, получим систему уравнений:
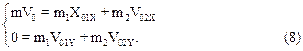
Из первого уравнения следует, что V02X=2V0. Подставляя найденное выражение в уравнение (6), получим для L
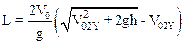 ,
,
где (как следует из второго уравнения системы (8)) V02Y= - V01Y, определенному соотношением (4).
Окончательно имеем:
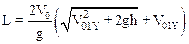 .
.
Расчеты дают L=1600 м.
Пример 6.3.
Электропоезд, имеющий массу М, двигаясь под уклон из состояния покоя, за небольшой промежуток времени Dt приобрел скорость V. Угол наклона дороги по отношению к горизонту равен a, коэффициент трения равен m. Найти работу силы тяги. Сопротивлением воздуха пренебречь.
Решение
| AF=? M Dt V0=0 V a m | 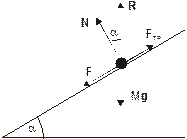
|
А. Решение этой задачи можно провести, используя определение работы:
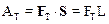 (1)
(1)
Величины FT и L найдем из системы кинематических уравнений
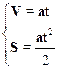
и уравнения движения электропоезда:
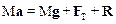 .
.
Запишем уравнения системы в проекциях на оси координат:
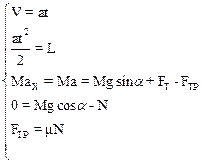
Решая систему, получим: для ускорения a=V/t, для пройденного пути L=Vt/2, для силы трения FTP=mN=mMgcosa. Сила тяги равна
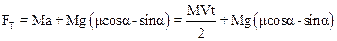 .
.
Подставляя в формулу (1), окончательно получим:
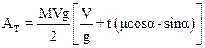 .
.
В. Решение этой задачи можно провести, используя закон изменения механической энергии. При движении поезда его энергия изменяется так, что DЕ=АВНЕШ.
Энергия поезда Е1 в начальном состоянии равна mgh1, в конечном состоянии Е2=mgh2+mV2/2. Таким образом:
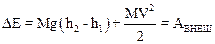 . (1)
. (1)
Работа внешних сил складывается из работы силы тяги и работы силы трения
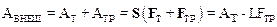 , (2)
, (2)
здесь L – пройденный при разгоне путь, FT и FTP численные значения силы тяги и трения.
Для определения неизвестных величин запишем систему уравнений
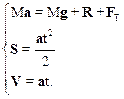
В проекции на оси координат она принимает вид
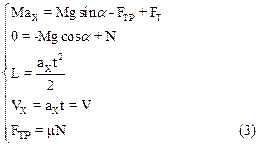
Из формулы (2) следует, что
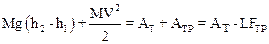 ,
,
откуда
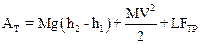 (4)
(4)
Решая систему (3), найдем, что: a=V/t, L=Vt/2, h=h2-h1=-Lsina, FTP=mN=mmgcosa.
Подставляя найденные выражения в (4), имеем окончательно для АТ:
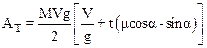 .
.
Дата добавления: 2015-08-08; просмотров: 4667;
