Построение разверток пирамидальной и конической поверхности

Построение разверток пирамидальных поверхностей сводится к многократному построению натурального вида граней – треугольников, из которых состоит данная пирамидальная поверхность. Развертка боковой поверхности конуса в общем случае строится по схеме развертки поверхности пирамиды, вписанной в данную коническую поверхность и заменяющую ее.

Пример 1. Построить развертку боковой поверхности наклонной треугольной пирамиды SABC (рис. 12.2).

Развертку боковой поверхности пирамиды строим по следующей схеме:

1. Определяем длины ребер и сторон основания пирамиды.

2. Строим на плоскости чертежа последовательно по трем сторонам
треугольники (грани пирамиды), примыкающие друг к другу и с общей
вершиной.

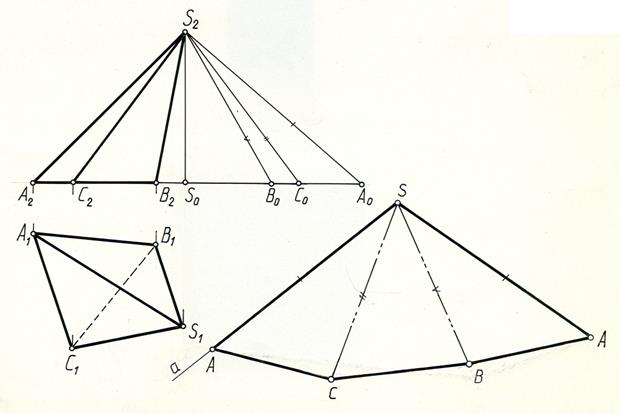
рис. 12.2

Решение. Как видно из чертежа, основание ABC пирамиды расположено в горизонтальной плоскости и поэтому его стороны на П₁ проецируются в натуральную величину. Натуральные размеры боковых ребер определяем с помощью прямоугольных треугольников, у которых одним катетом является превышение точки S над точками А, В, С (отрезок S₂S₀), a вторым катетом отрезок, равный горизонтальной проекции соответствующего бокового ребра (S₀A₀=S₁A₁, S₀B₀=S₁B₁, S₀C₀= S₁C₁). Натуральной величиной боковых ребер являются отрезки S₂A₀, S₂B₀, S₂C₀. После определения натуральных величин ребер приступаем к построению развертки. Для этого из произвольной точки S проводим произвольную прямую а. Откладываем на ней от точки S-SA=S₂A₀. Из точки А проводим дугу радиусом A₁C₁,а из точки S-дугу радиусом S₂C₀.Пересечение дуг определяет положение вершины В треугольника SАВ-натуральной величины грани пирамиды. Аналогично находим точки B и А. Соединив точки А С В A S, получим развертку боковой поверхности пирамиды SABC.

Пример 2. Построить развертку боковой поверхности наклонного эллиптического конуса с круговым основанием (рис. 12.3).

Развертка конической поверхности выполняется по схеме построения развертки боковой поверхности пирамиды, способу треугольников. Для этого коническая поверхность аппроксимируется (заменяется) вписанной в нее многогранной пирамидальной поверхностью.

Решение. В данную коническую поверхность впишем двенадцатиугольную пирамиду. Так как коническая поверхность имеет плоскость симметрии Г, то можно построить развертку только одной половины поверхности. Разделим половину окружности на 6 равных частей, начиная от точки (O₁) пересечения ее с плоскостью симметрии Г (Г₁), которая делит поверхность и, следовательно, ее развертку на 2 симметричные части. Через точки деления O₁l₁, 2₁ ... и вершину S₁ проводим горизонтальные проекции образующих конуса- прямые S₁O₁, S₁1₁, S₁2₁ ..., которые являются боковыми ребрами вписанной пирамиды. Сторонами основания пирамиды являются хорды, соединяющие точки деления и проецирующиеся на П₁ в натуральную величину. Натуральную величину боковых ребер определяем способом прямоугольных треугольников. Проводим ось симметрии развертки и от точки S откладываем отрезок SO=S₂О₀ (pиc. 11.3). Из точки S радиусом S₂1₀ проводим дугу окружности, а из точки О радиусом О₁1₁делаем на ней засечку. Точка 1 – искомая точка развертки. Для построения смежной грани из точки S радиусом S₂2₀, а из точки 1 радиусом 1₁2₁ сделаем засечки и в пересечении отметим точку 2 и т.д. Соединив точки 0,1, 2 ... 6 плавной кривой получим развертку ½ боковой поверхности конуса.

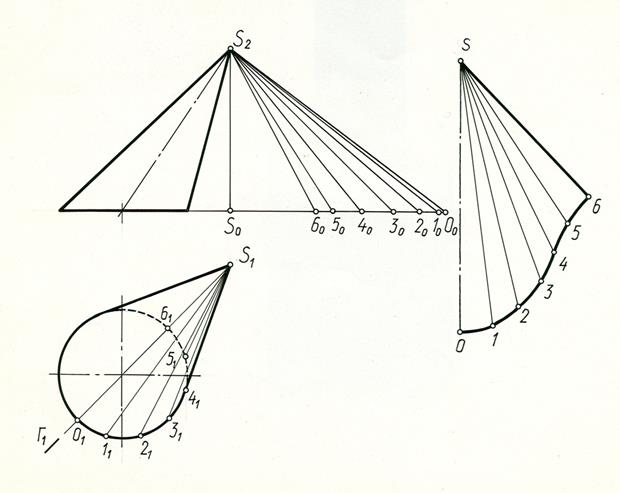
Рис. 12.3

Построение разверток призматических и цилиндрических поверхностей.

Построение разверток призматических поверхностей сводится к построению истинных размеров и формы отдельных граней, что и выполняется на чертеже различными способами. Построение разверток цилиндрических поверхностей соответствует построению разверток призматических поверхностей вписанных в цилиндрическую поверхность.