Общие понятия. В практике инженерного проектирования и строительства часто возникает необходимость моделировать поверхность плоской фигурой

В практике инженерного проектирования и строительства часто возникает необходимость моделировать поверхность плоской фигурой, которая может быть названа «выкройкой» поверхности или разверткой. Разверткой поверхности называется плоская фигура, в которую преобразуется поверхность при ее совмещении с плоскостью. При этом поверхность представляется в виде гибкой, но нерастяжимой и несжимаемой пленки.

Построение разверток поверхностей является технической задачей, имеющей большое значение при изготовлении различных деталей и конструкций из листового материала, например: воздуховодов для промышленной вентиляции, водосточных труб, кожухов, цистерн, различных отводов.

Для обеспечения необходимой точности изготовления и экономичного расходования материала изделие конструируют таким образом, чтобы каждая часть изделия была развертывающейся поверхностью.

Развертывающейся поверхностью называется поверхность, которая всеми своими точками может быть совмещена с плоскостью, т.е. деформирована в плоскость без складок и разрывов. Каждой точке на поверхности соответствует единственная точка развертки, т.е. поверхность и ее развертку можно рассматривать как две геометрические фигуры, между точками которых существует взаимнооднозначное соответствие, обладающие свойствами:

1. Длины отрезков линий, расположенных на поверхности и на ее развертке, равны между собой.

2. Углы между соответствующими линиями поверхности и развертки равны между собой.

Однако, угол между двумя образующими на конической поверхности меньше угла между соответствующими им прямыми на развертке, так как вершина конуса является особой точкой, и она не обладает свойствами, которые характерны обыкновенным точкам.

3. Площади фигур, ограниченные соответствующими замкнутыми линиями на поверхности и развертке равны между собой. Следует помнить, что все размеры на развертке имеют натуральную величину.

Рассмотрим поверхность θ₀ и ее развертку θ (рис. 12.1). Длина дуги АВ равна длине дуги А₀В₀, угол α равен углу α₀, и площадь F равна площади F₀. Заметим, что углом между двумя кривыми называется угол между их касательными. Прямой линии на поверхности (образующей) всегда соответствует прямая на развертке, параллельные прямые на поверхности переходят на развертке в параллельные.

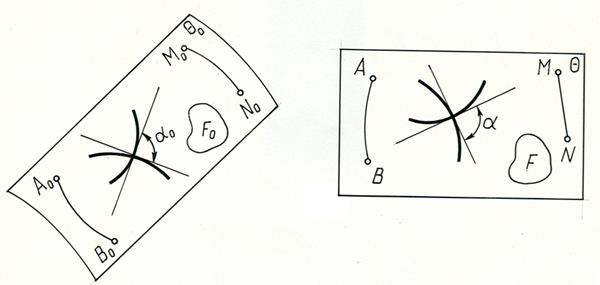
Рис. 12.1

Линия кратчайшего расстояния между двумя точками на поверхности называется геодезической. На развертке этой линии соответствует прямая. Например, дуга M₀N₀ является кратчайшей из всех дуг на поверхности, проведенных между точками M₀N₀, тaк как на развертке этой линии соответствует прямая MN.