Тип 1 . Построить касательную плоскость к поверхности через точку на ней.
Задача 1. Построить плоскость, касательную к поверхности сферы в точке К (рис. 11.2) .
Выберем две кривые линии, проходящие через точку К. Целесообразно взять наиболее графически простые линии – окружности (параллели и меридианы) – n и m.
К этим двум окружностям в точке К проводим касательные, причем каждую в плоскости своей окружности, т.е. t лежит в вертикальной, а t′ – в горизонтальной плоскостях.
Построенные касательные t и t′ и задают искомую касательную плоскость.
В рассматриваемой задаче точка К- эллиптическая точка касания. ОК - радиус, являющийся нормалью к касательной плоскости в точке К. Построенная плоскость ему перпендикулярна.

Рис. 11.2
Задача 2. Построить касательную плоскость к поверхности вращения
в точке К ( рис. 11.3).
В качестве линий, задающих касательную плоскость, примем две
прямые, одна из которых является касательной к окружности - параллели, проходящей через точку К, вторая – касательной к меридиану, проходящему через эту же точку.
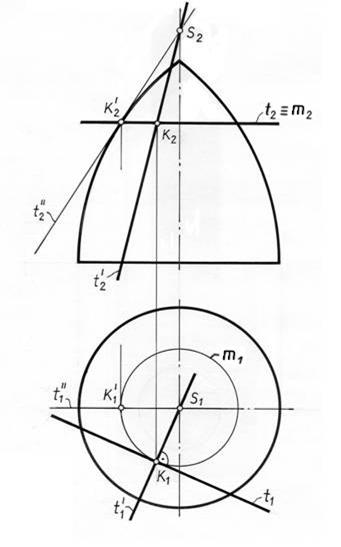
Рис . 11.3
Для того, чтобы провести касательную к меридиану, повернем его до
совмещения с главным меридианом и проведем касательную t′′ 2 в точке
К′2 , лежащей на той же окружности параллели, что и точка К, до пересечения с осью симметрии фигуры в точке S. Через эту же точку S пройдет касательная t′ 2 после возвращения поворачиваемого меридиана в исходное состояние. Для ее построения соединяем S2 и К2 .
Вторая касательная t строится таким образом. Ее фронтальная проекция t 2 на фронтальной плоскости проекций совпадает с проекцией окружности параллели m. Горизонтальная проекция t 1 строится как касательная прямая к горизонтальной проекции окружности – параллели m1.
Касательные t′ и t′ и определят искомую касательную плоскость.
Отметим, что в этой задаче точка касания К также представляет собой эллиптическую точку касания.
Задача 3.Построить касательную к цилиндру в точке К ( рис. 11.4).
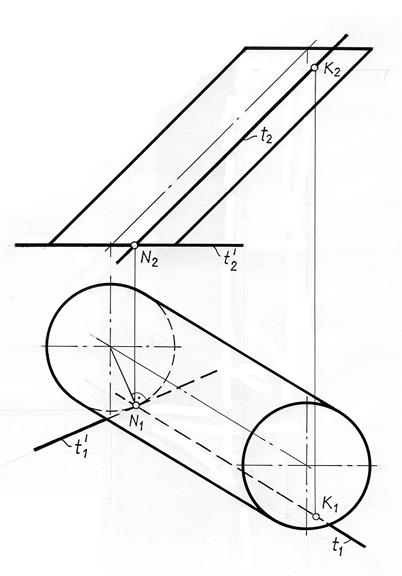
Рис. 11.4
Элементом касания плоскости к цилиндру будет являться образующая цилиндра t , на которой лежит точка К. В этой задаче точка касания К является одной из геометрического множества параболических точек касания, лежащих на одной образующей цилиндра. С этой образующей совпадает первая касательная прямая t к этой поверхности.
Вторая касательная прямая пройдет через точку N, лежащую в основании цилиндра. Эта точка является точкой пересечения образующей t с плоскостью основания цилиндра.
Построенные касательные прямые t и t ′ и образуют касательную плоскость к цилиндру в точке К.
Дата добавления: 2015-07-10; просмотров: 1166;
