Плоскостям проекций
Вращение вокруг осей, перпендикулярных плоскостям проекций, является частным случаем плоскопараллельного перемещения; все точки геометрической фигуры перемещаются в пространстве также в плоскостях, параллельных плоскостям проекций, но не по произвольной траектории, а по окружностям.
Сущность способа заключается в том, что проецируемую фигуру путем поворота ее вокруг выбранной оси приводят относительно плоскостей проекций в новое положение, при котором легко получить решение задачи.
Все точки геометрической фигуры, не лежащие на оси вращения, вращаются в плоскостях, перпендикулярных оси вращения (рис. 10.9): Σ^i; AÎΣ . Центр О окружности m, которую описывает точка А , является точкой пересечения оси i с плоскостью Σ ; O= i∩Σ. Отрезок АО является радиусом R окружности m.
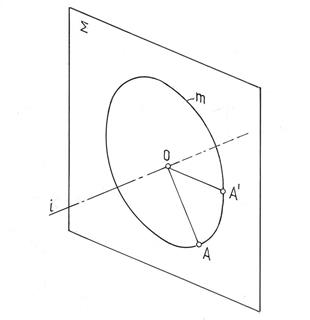
Рис. 10.9
Рассмотрим, как изменяется положение проекций точки при вращении ее вокруг оси, перпендикулярной к плоскости П1 (рис. 10.10).
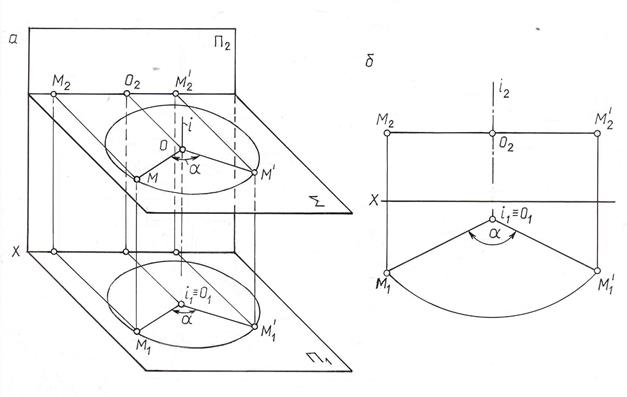
Рис. 10.10
При вращении точки М вокруг оси i^П1 (центр вращения О, радиус вращения ОМ^i) на угол a , ее горизонтальная проекция М1 перемещается по окружности (с центром в точке О1 @ i1) того же радиуса, в ту же сторону и на тот же угол a , что и сама точка М. Траектория движения точки М в пространстве на плоскость П1 проецируется без искажения, т.к. она принадлежит плоскости Σ, параллельной П1. Фронтальная проекция точки М(М2) перемещается по прямой, параллельной оси ОХ.
Вращение геометрических фигур сводится к вращению конечного числа точек, определяющих данную фигуру. При этом полезно иметь в виду следующее:
а) точки, лежащие на оси вращения, не меняют своего положения, остальные точки вращаются в плоскостях, перпендикулярных оси вращения;
б) все вращающиеся точки поворачиваются в одну сторону на один и тот же угол;
в) если ось перпендикулярна некоторой плоскости проекций, то проекции на эту плоскость вращающейся фигуры в любом ее положении конгруэнтны. Последнее вытекает из рассмотренных свойств метода плоскопараллельного перемещения, т.к. вращение вокруг осей, перпендикулярных к плоскостям проекций представляет собой частный случай этого метода.
Рассмотрим, как осуществляется на эпюре перемещение отрезка общего положения в частное положение путем вращения вокруг оси перпендикулярной плоскостям проекций.
Пример 1. Отрезок АВ общего положения преобразовать в положение параллельное плоскости проекций П2.
Чтобы осуществить такое преобразование, достаточно повернуть отрезок АВ вокруг оси i ^ П1 на угол a. Для сокращения количества геометрических построений ось i ∋ В (рис. 10.11).
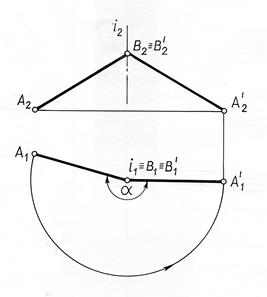
Рис. 10.11
Величина угла a принимается такой, чтобы после поворота горизонтальная проекция отрезка заняла положение || ОХ. Так как точка В принадлежит оси вращения, то она не будет менять своего положения в процессе преобразования, следовательно, В1 º В1// и В2 º В2//. Для нахождения точки А2/ необходимо из А1// провести вертикальную линию связи и отметить точку пересечения ее в горизонтальной прямой, проведенной через А2.
Дата добавления: 2015-07-10; просмотров: 747;
