Плоскостей проекций

Задача 1. Преобразовать эпюр, изображенный на рис. 9.9 так, чтобы прямая общего положения оказалась параллельной одной из плоскостей проекций новой системы.

Для решения задачи необходимо расположить новую плоскость проекций параллельно заданному отрезку (П₄║АВ). Тогда на эту плоскость проекций отрезок проецируется без изменений.

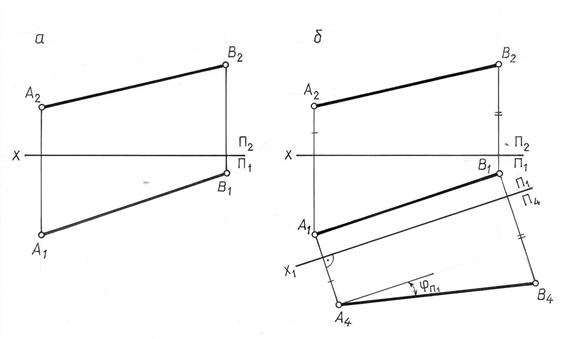
Рис. 9.9

Решение этой задачи показано на рис. 9.9,б. Параллельно А₁ В₁ проведена ось Х₁, и в системе плоскостей проекций 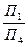построена новая фронтальная проекция отрезка А₄В₄. Очевидно, что /А₄В₄/=/АВ/ и угол φ, образованный проекцией А₄В₄ с осью Х₁ равен углу наклона прямой АВ к плоскости П₁.

Задача 2. Преобразовать эпюр, изображенный на рис. 9.10 так, чтобы отрезок АВ прямой линии общего положения оказался перпендикулярным одной из плоскостей проекций.

Для решения задачи нужно произвести последовательно две замены плоскостей проекций:

1) систему 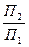заменяем системой 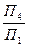, расположив плоскость П₄ параллельно АВ;

2) от системы 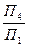переходим к 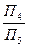, расположив плоскость П₅ перпендикулярно прямой АВ. Выполненные построения приведены на рис. 9.10.

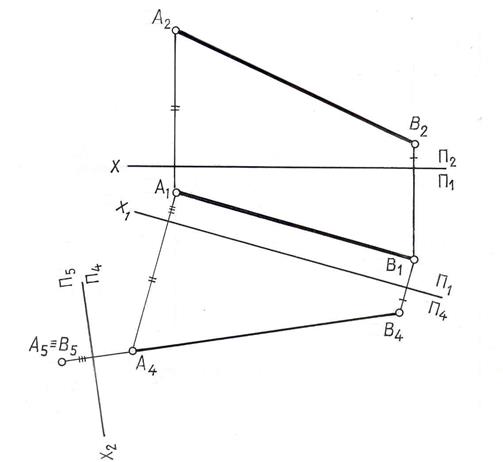
Рис. 9.10

Задача 3. Преобразовать плоскость общего положения в проецирующую.

Для решения данной задачи необходимо ввести новую плоскость проекций так, чтобы она была перпендикулярна заданной плоскости Γ(АВС) и одной из плоскостей проекций, т.е. перпендикулярна линии их пересечения. Линией пересечения плоскости Γ с плоскостью проекций является соответствующий след плоскости Γ. Поэтому новая плоскость проекций должна быть перпендикулярна одному из следов данной плоскости или одной из ее линий уровня, которая параллельна соответствующему следу.

На рис.9.11 показано преобразование плоскости Γ(АВС) в проецирующую. Для этого в плоскости Γ проведена горизонталь h(h₂h₁) и перпендикулярно к ней, а, следовательно, и ко всей плоскости Γ введена новая плоскость П₄, для чего ось Х₁ новой системы плоскостей проекций 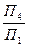проведена перпендикулярно горизонтальной проекции горизонтали Х_1┴h_1, и в соответствии с известным правилом построена новая проекция А₄В₄С₄ треугольника АВС, представляющая отрезок прямой линии. После проведенных построений плоскость Γ(АВС) оказалась перпендикулярной плоскости проекций П₄ и с плоскостью П₁ составляет угол a.

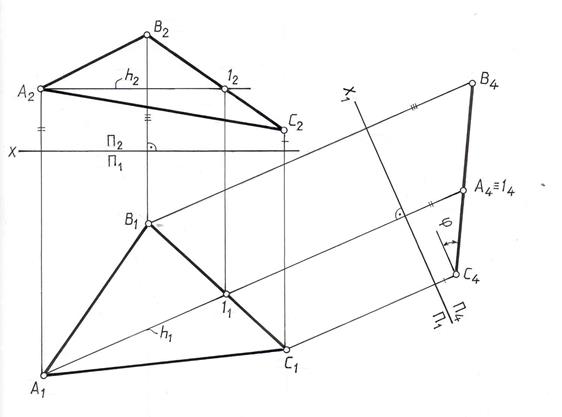
Рис. 9.11

Задача 4. Преобразовать плоскость общего положения Γ(АВС) в плоскость уровня.

Преобразование плоскости общего положения в плоскость уровня производится последовательно двумя заменами плоскостей проекций - вначале плоскость общего положения преобразуется в проецирующую, затем полученная проецирующая плоскость преобразуется в плоскость уровня.

На рис.9.12 для преобразования плоскости Γ в проецирующую введена новая плоскость проекций П₄ , перпендикулярная плоскости Γ. Ось новой системы плоскостей 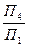проведена перпендикулярно горизонтальной проекции горизонтали. Полученная проекция А₄В₄С₄ является вырожденной проекцией плоскости Γ, т.к. плоскость Γ является проецирующей по отношению к плоскости П₄.

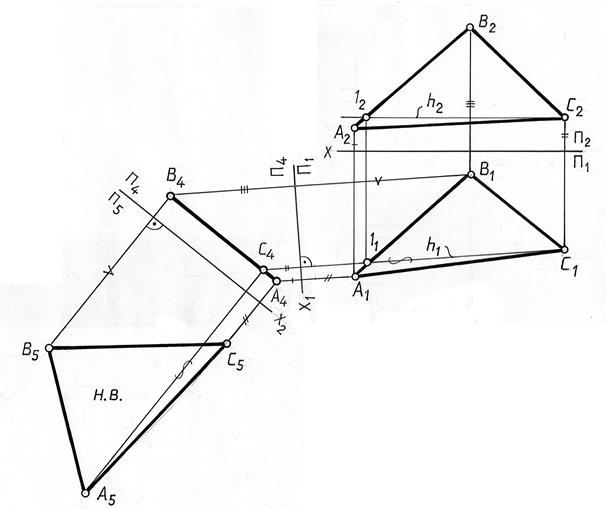
Рис. 9.12

Для преобразования проецирующей плоскости в плоскость уровня введена новая плоскость проекций П₅ , параллельная плоскости Γ. Ось Х₂ новой системы плоскостей проекций 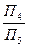параллельна вырожденной проекции А₄В₄С₄ плоскости Γ. При построении новой проекции А₅В₅С₅ использованы расстояния от заменяемых проекций А₁В₁С₁ до оси Х_1. Так как в новой системе плоскостей проекций 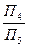плоскость Γ(АВС) является параллельной плоскости П₅ , то на эту плоскость проекций она проецируется в натуральную величину.

Рассмотренные четыре основные задачи лежат в основе решения многих других задач способом замены плоскостей проекций. Рассмотрим примеры решения некоторых задач.

Пример 1. Преобразовать плоскость Γ общего положения, заданную следами, в проецирующую (рис. 9.13).

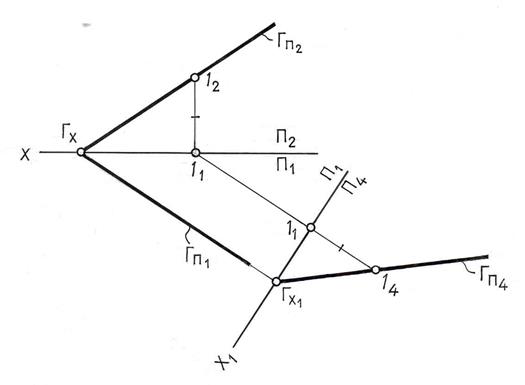
Рис. 9.13

Плоскость Γ преобразуем во фронтально-проецирующую. Известно, что горизонтальный след фронтально-проецирующей плоскости перпендикулярен оси Х, следовательно новую ось Х₁ проводим перпендикулярно к Γ_П1. Через точку, в которой Γ_П1∩ Х_{1 =} Γ_Х1 пройдет фронтальный след Γ_П4. Для определения его направления достаточно найти одну точку. В качестве такой точки можно взять произвольную точку 1∈Γ и указать ее фронтальную проекцию 1₄ на новой плоскости П_4. Через Γ_Х1 и 1₄ проводим Γ_П4.

Пример 2. Определить расстояние от точки Т до плоскости Σ общего положения, заданной DАВС (рис. 9.14)

Плоскость Σ(АВС) преобразуем в проецирующую, для чего в плоскости построим горизонталь h(h₂h₁). Перпендикулярно горизонтальной проекции горизонтали проведем ось Х₁ новой системы плоскостей проекций 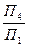. Строим новые проекции точек А₄В₄С₄ , откладывая расстояния от оси Х₁, равные расстояниям от заменяемых проекций А₂В₂С₂ до оси Х.

Плоскость Σ(АВС) оказалась перпендикулярной плоскости проекций П₄ и спроецировалась на эту плоскость в прямую линию. На плоскость П₄ переносим точку Т(Т₄) и опускаем перпендикуляр на плоскость D (АВС) . Т₄К_{4 ┴}(А₄В₄С₄) , где К – основание перпендикуляра. Расстояние от точки Т до плоскости DАВС на плоскости П₄ проецируется без искажения. |Т₄К₄|= |ТК|. Возвращаем проекции перпендикуляра на плоскость 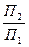, для этого из точки Т₁ проводим проекцию перпендикуляра Т₁К₁ параллельно оси Х₁ и перпендикулярно h₁. Дальнейшие выполненные построения показаны на рис. 9.14.

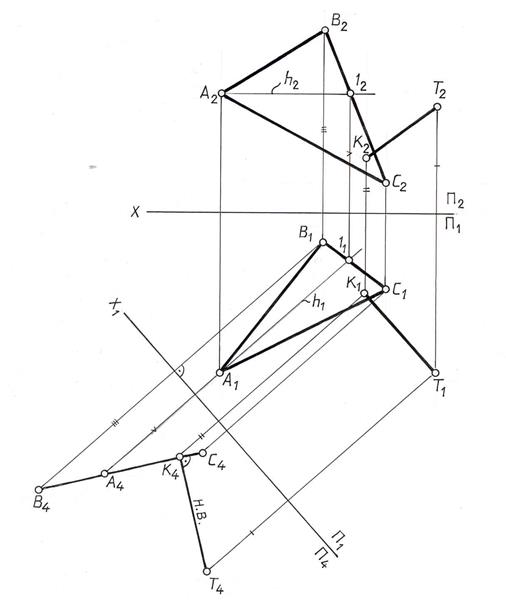
Рис. 9.14

Лекция 10

Способы преобразования проекций и их

применение к решению задач