Тип 2. Построить плоскость, касательную к конической поверхности и проходящую через точку К, не принадлежащую поверхности конуса.

В качестве двух линий на заданной поверхности выберем две прямые - образующие конуса и окружность – параллель m, расположенную на высоте точки К (рис. 11.5).

Задача может иметь два решения, поскольку к окружности – параллели m из точки К можно провести две касательные прямые t и t′ . Эти касательные на фронтальной проекции совпадают в одну прямую ( t ₂ ≡ t′ ₂), совпадающую с фронтальной проекцией окружности – параллели m ₂.

В точках касания прямых t и t′ проведем образующие конуса а и в , по которым две искомые касательные плоскости касаются конической поверхности.

Таким образом, первая касательная плоскость задается образующей а и касательной t, которые пересекаются в точке 1. Вторая касательная плоскость задается образующей в и касательной t′, пересекающихся в точке 2.

Отметим, что все точки касания обеих касательных плоскостей с конической поверхностью также относятся к параболическим.

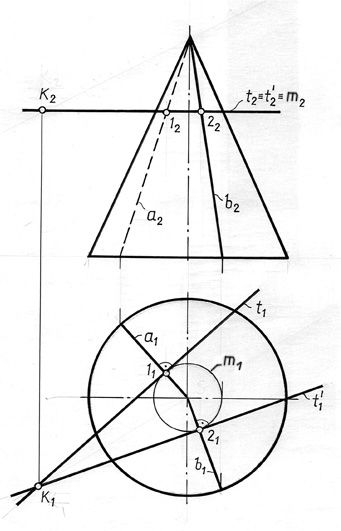
Рис. 11.5