Тип 3. Построить плоскость, касательную к цилиндру и параллельную прямой l.
Задачу решаем способом построения касательного следа плоскости параллельно следу плоскости параллелизма (рис. 11.6). Элементом касания цилиндра с касательной плоскостью является образующая прямая линия.
Заключим прямую l в плоскость параллелизма, параллельную образующим цилиндра. Для этого на прямой l берем произвольную точку К и проводим через нее линию m , параллельную образующим цилиндра. Пересекающиеся прямые линии l и m определяют плоскость параллелизма – плоскость R.
Строим линию пересечения плоскости R с плоскостью основания цилиндра – линию m. Она проходит через точки А и В.
Касательная плоскость параллельна плоскости параллелизма R и поэтому будет пересекаться с основанием по прямой, параллельной прямой m. Кроме того, она должна касаться линии основания цилиндра.
Таких прямых можно провести две ( t и t′ ) . Поэтому задача имеет два решения. Обе построенные прямые касаются основания цилиндра в точках 1 и 2. Отметим две образующие - n и n′, по которым искомые плоскости касаются поверхности цилиндра.
Задача имеет два решения. Каждая из образующих n и n′ в сочетании с одной из касательных t или t′ определяет одну из двух касательных плоскости.
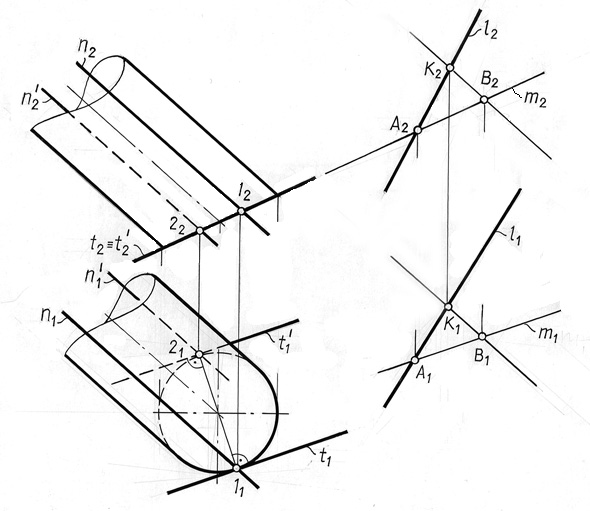
Рис. 11.6
Тип 4. Провести касательную плоскость к сфере параллельно заданной плоскости Σ ( рис. 11.7).
Плоскость Σзадана фронталью f и горизонталью h. Решением задачи будут две плоскости, параллельные заданной и касающиеся сферы в двух точках, лежащих на концах одного диаметра сферы, который перпендикулярен заданной плоскости Σ.
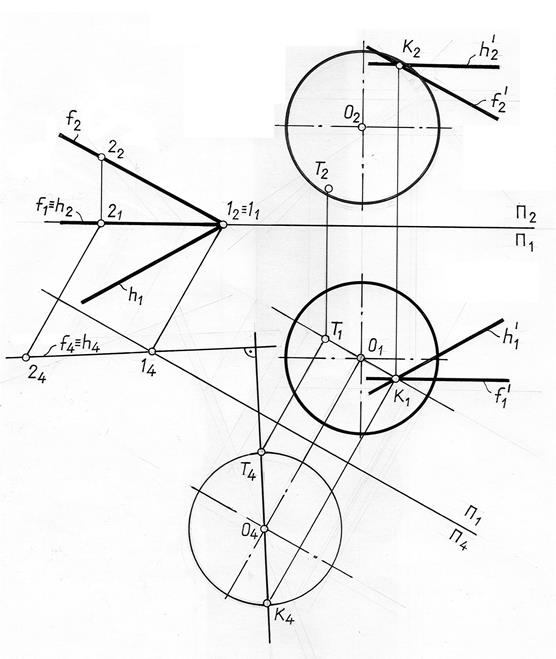
Рис. 11.7
Определим эти точки касания. Для этого произведем преобразование чертежа любым методом (например, заменой плоскостей проекций). Проведем новую плоскость проекций П4 так, чтобы заданная плоскость Σ стала проецирующей.После этого из центра новой проекции сферы на плоскости - точки О4 проведем перпендикуляр к вырожденной проекции плоскости Σ.
Пересечение этого перпендикуляра с очерком сферы даст Т и К, которые и будут искомыми точками касания.
Через полученные точки проводим две касательные плоскости, используя условие их параллельности плоскости Σ.
На рис. 11.7 показана лишь одна касательная плоскость, проведенная через точку К.
Тип 5. Провести плоскость, касательную к поверхности цилиндра через прямую l , лежащую вне этой поверхности ( рис. 11.8 ).
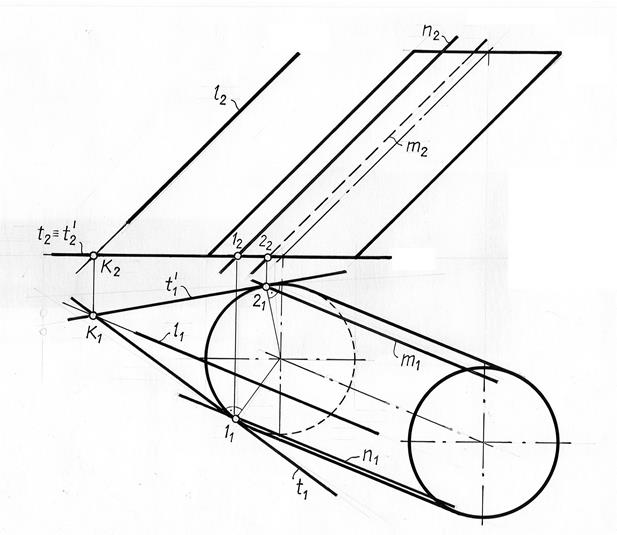
Рис. 11.8
При этом надо иметь в виду, что построение такой плоскости возможно только в следующих случаях:
при цилиндрической поверхности – если заданная прямая параллельна образующим или касается этой поверхности.
при конической поверхности – если прямая параллельна образующим или проходит через его вершину.
При сферической поверхности - всегда, когда прямая не пересекает поверхность сферы.
Определяем точку пересечения прямой l с плоскостью основания
цилиндра - точку К. Через эту точку проводим две прямые t′1 и t 1 , касательные к проекции основания цилиндра - окружности. Их фронтальные проекции t′2 и t 2 совпадают с фронтальной проекцией основания цилиндра.
Отмечаем точки касания этих прямых с проекцией основания цилиндра – точки 1 и 2. Из этих точек строим проекции образующих m и n , по которой искомые касательные плоскости касаются заданной поверхности.
Каждая из этих образующих совместно с одной из касательных t′ и t
задает касательную плоскость.
Лекция 12
Развертки поверхностей
Общие понятия. Развертывающиеся и неразвертывающиеся поверхности.
Общие правила построения разверток. Построение разверток пирамидальной, конической, призматической и цилиндрической поверхностей. Построение приближенных разверток неразвертывающихся поверхностей
Дата добавления: 2015-07-10; просмотров: 1760;
