Способ нормального сечения

1. Для получения нормального сечения проводится плоскость
перпендикулярная к боковым ребрам призмы.

2. Определяется натуральная величина нормального сечения. Стороны этого сечения определяют расстояние между боковыми ребрами, т.е. ширину граней.

3. Нормальное сечение разворачивается в прямую и через концы отрезков проводятся ребра призмы, которые перпендикулярны построенной прямой, а следовательно и к периметру 1,2,3 сечения.

4. На проведенных ребрах откладываются длины отрезков боковых ребер, заключенных между линией сечения и основаниями. Полученные точки соединяются последовательно между собой.

Пример 4. Построить полную развертку наклонной треугольной призмы (рис. 12.5).

Призма расположена относительно плоскостей проекций так, что ее боковые ребра параллельны фронтальной плоскости проекций и проецируются на П₂ в натуральную величину. Стороны основания проецируется без искажения на плоскость П₁. Пересечем призму в произвольном месте плоскостью Г перпендикулярной боковым ребрам.

В нашем примере эта плоскость является фронтально-проецирующей плоскостью и пересекает призму по треугольнику 1 2 3. (1₂2₂3₂, 1₁2₁3₁) Стороны треугольника определяют расстояние между боковыми ребрами. Определяем натуральную величину сечения (треугольник A₄B₄C₄), используя способ замены плоскостей проекций. Стороны нормального сечения; последовательно отложим на прямой а: 1-2=1₄-2₄, 2-3=2₄-3₄, 3-1=3₄-1₄. Полученный отрезок 1-1 равен периметру нормального сечения.

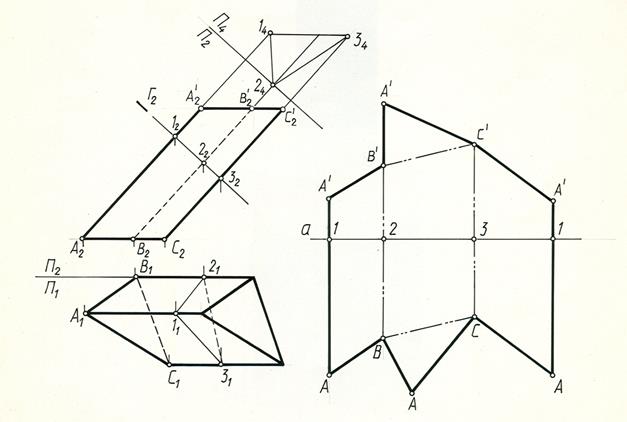
Рис. 12.5

Через точки 1, 2, 3 проведем прямые перпендикулярные к, развертке периметра сечения и на них отложим натуральную величину боковых ребер 1А=1₂А₂ и 1А'=1₂А₂' , 2В=2₂В₂ и 2В'=2₂В₂', ЗС=3₂С₂ и ЗС'=3₂С₂' и т.д. Соединив концы отложенных отрезков, получим развертку боковой поверхности призмы. Для построения полной развертки необходимо к развертке боковой поверхности пристроить натуральные величины оснований, используя натуральные величины их сторон.