Решение. Применив метод сечений, вырезаем узлы и и, заменив действие отброшенных частей системы силами (рис.2.47
Применив метод сечений, вырезаем узлы 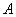 и
и 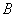 и, заменив действие отброшенных частей системы силами (рис.2.47, б), составляем уравнения равновесия сил для каждого узла
и, заменив действие отброшенных частей системы силами (рис.2.47, б), составляем уравнения равновесия сил для каждого узла
для узла 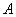
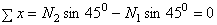 , откуда
, откуда 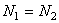 ;
;
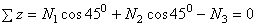 ;
;
для узла 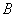
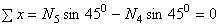 , откуда
, откуда 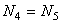 ;
;
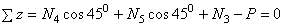 .
.
Имеем четыре уравнения равновесия и пять неизвестных сил, следовательно, система один раз статически неопределима.
Рассмотрим геометрическую сторону задачи. При нагружении системы силой 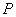 все ее стержни растягиваются и деформированная система занимает положение, показанное штриховыми линиями на рисунке 2.47, а.
все ее стержни растягиваются и деформированная система занимает положение, показанное штриховыми линиями на рисунке 2.47, а.
Если бы стержень 3 был абсолютно жестким, то при деформации системы перемещения узлов 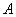 и
и 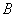 были бы одинаковыми. Так как стержень 3 растягивается, перемещение узла
были бы одинаковыми. Так как стержень 3 растягивается, перемещение узла 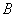 больше перемещения узла
больше перемещения узла 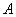 на удлинение этого стержня
на удлинение этого стержня
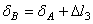 .
.
Из схемы, представленной на рисунке 2.47, а, находим соотношение между перемещениями узлов и деформациями стержней
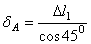 ;
; 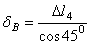 .
.
Запишем уравнение перемещений через деформации стержней
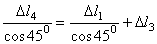 .
.
Используя закон Гука, выразим деформации стержней через действующие в них продольные силы
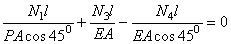
или
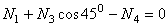 .
.
Решив полученное уравнение совместно с уравнениями равновесия, находим
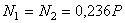 ;
; 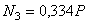 ;
; 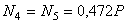 .
.
Дата добавления: 2015-08-08; просмотров: 668;
