Раскрытие статической неопределимости

Операции по определению неизвестных силовых факторов в статически неопределимых системах принято называть раскрытием статической неопределимости. Производятся они следующим образом. В начале исходя из силовой схемы составляются уравнения равновесия.

При решении любых задач число уравнений должно быть равно числу неизвестных. Для определения сил в стержнях статически неопределимых систем следует составлять уравнения, дополняющие уравнения равновесия до числа неизвестных сил. Дополнительные уравнения, называемые уравнениями совместности перемещений или деформаций, составляют, определяя перемещения отдельных стержней системы и устанавливая между ними связь.

Принцип совместности деформирования выражает условие, заключающееся в том, что конструкция должна деформироваться без разъединения и непредусмотренного взаимного перемещения отдельных ее звеньев.

Для облегчения записей уравнений перемещений строят схему деформаций всех упругих элементов или схему деформированной системы. Для любой статистически неопределимой системы всегда можно составить столько дополнительных уравнений, сколько раз система статически неопределима.

В силу различной взаимозависимости элементов, различия накладываемых связей и условий деформирования, уравнения совместности деформаций систем записываются по разному. Но все они выражают соотношения деформаций (перемещений) отдельных упругих элементов системы. Например, на схеме,

на рис. 2.40, в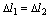

а на рис. 2.40, г.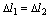

т. к. весь стержень не может не удлиниться, ни укоротиться. На схеме (рис. 2.40, а) можно установить геометрическое соотношение деформаций стержней 1, 2 и 3.

После получения указанных геометрических соотношений величины абсолютных изменений, длины стержней 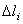заменяют по закону Гука их выражениями через усилия :

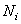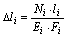
Полученные таким образом уравнения, содержащие в качестве неизвестных продольные силы, и являются дополнительными уравнениями. Они включают также показатели жесткости отдельных звеньев конструкции, вводя тем самым зависимость распределения сил внутри системы от жесткости ее элементов. Вместе с уравнениями статистики общее число уравнений равно числу неизвестных сил. Решая их, определяют неизвестные внутренние (продольные) силы.

В заключение может быть выполнена энергетическая проверка решения задачи. Она заключается в составлении и удовлетворении равенства работы внешних сил А и суммы потенциальной энергии деформации элементов системы U.

Сложные статически неопределимые системы, в том числе статически неопределимые фермы (элементы ферм работают на растяжение, сжатие) и статически неопределимые рамы, рассматриваются в курсе строительной механики стержневых систем. В курсе сопротивления материалов рассматриваются обычно простейшие статически неопределимые системы, к которым относятся:

а) прямые стержни постоянного, кусочно-постоянного и переменного сечений, закрепленные с двух сторон, от нагрузки действующей вдоль оси стержня;

б) системы шарнирно соединяемых стержней с возможным включением жестких недеформируемых элементов.

При решении статически неопределимых систем, в стержнях которых действуют продольные силы, можно отметить основные этапы:

1) анализ работы конструкции с указанием действующих силовых факторов и выяснением деформации ее элементов, определение степени статической неопределимости;

2) статическая сторона задачи – составляют уравнения равновесия для системы или отсеченных ее частей;

3) геометрическая сторона задачи – выясняют, как деформируются стержни системы, изображают систему в деформированном виде, устанавливают связи между перемещениями отдельных элементов системы, составляют уравнения совместности перемещений;

4) физическая сторона задачи – выражает деформации элементов, согласно закону Гука, через действующие в них неизвестные усилия;

5) синтез – определяют неизвестные силы, решая совместно систему уравнений равновесия и перемещений.

Статически неопределимые конструкции характеризуются рядом осо­бенностей, по сравнению со статически определимыми системами. Так, при эксплуатации конструкции возможно изменение ее температуры, вызванное условиями работы или сменой времен года. С изменением температуры изменяются линейные размеры элементов конструкции: увеличиваются при нагреве, уменьшаются при охлаждении на величину

, (2.38)

где - температурный коэффициент линейного расширения (см. раздел «Справочные данные»); 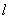- длина элемента; 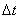- изменение температуры, (⁰С).

В статически определимых системах длина стержня может свободно изменяться при их нагреве или охлаждении (рис.2.41, а, б).

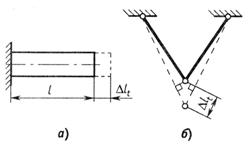
Рис.2.41

В статически неопределимых системах при изменении температуры возникают дополнительные силы. Если нагреть стержень, жестко закрепленный по концам (рис.2.42, а), то его длина не может изменяться: этому препятствуют жесткие заделки. В опорах (заделках) возникают реакции, сжимающие стержень.

Так как неизвестных сил две, а уравнение равновесия можно составить только одно: 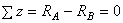, то система один раз статически неопределима.

Решая геометрическую часть задачи, составляем уравнение перемещений. Отбросим одну из опор и заменим ее действие неизвестной силой . Теперь стержень при нагреве может удлиниться на величину (рис.2.42, б).

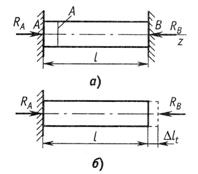
Рис.2.42

Так как длина стержня остается неизменной, перемещение сечения 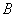должно быть равно нулю, следовательно, сила должна сжать стержень на величину, равную его удлинению при нагреве:

.

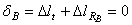Решая физическую часть задачи, с учетом равенства 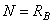получаем

.

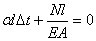Тогда продольная сила в сечениях стержня

;

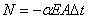напряжение в стержне

.

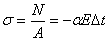Отметим, что напряжение в стержне не зависит от площади сечения.

Элементы конструкций изготовляют с определенной точностью. При сборке статически неопределимых систем, имеющих неточно изготовленные стержни, стержни приходится деформировать (удлинять или укорачивать), при этом в них возникают напряжения, называемыми начальными или монтажными.

Рассмотрим систему, один из стержней которой изготовлен короче, чем требуется, на величину (рис.2.43, а). Определим внутренние силы и напряжения, возникающие в стержнях системы при ее сборке. Стержни имеют одинаковые размеры и изготовлены из одного материала.

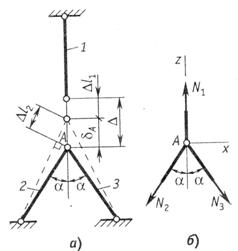
Рис.2.43

При сборке системы все три стержня необходимо удлинить, приложив к ним растягивающие силы. В собранном виде система показана штриховыми линиями (см. рис.2.43, а). Вырежем узел 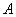(рис.2.43, б), составим уравнения равновесия сил

,

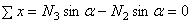откуда

;

.

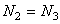Система один раз статически неопределима. Рассмотрим геометрическую часть задач и составим уравнение перемещений. Из схемы, представленной на рис.2.43, а, следует, что

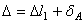, где .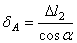

Уравнение перемещений принимает вид

.

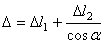Используя закон Гука, выразим удлинение через неизвестные силы в стержнях

.

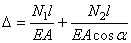Решив уравнение перемещений совместно с уравнениями равновесия, получим

; .

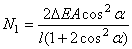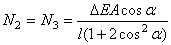Начальные напряжения часто специально создают в статически неопределимых системах, таких, например, как соединения с натягом и резьбовые соединения. Создавая в элементах статически неопределимой системы начальные напряжения, знак которых противоположен знаку напряжения от внешних сил, можно повысить прочность конструкции или увеличить допускаемую для нее нагрузку.

Распределение усилий между элементами системы зависит от их же­сткости. Если увеличить жесткость какого- либо элемента, то он примет на себя большее усилие. Изменяя соотношение жесткостей элементов конструкций, можно менять распределение усилий между ними.

Эти особенности статически неопределимых конструкций должны учитываться при проектировании или применении таких систем.

Статически неопределимые системы обладают повышенной «живуче­стью». Разрушение одного или нескольких элементов (в зависимости от числа дополнительных связей) не вызывает потерю несущей способности конструкции в целом. Так разрушение даже двух стержней в системе, показанной на рис.2.39, в не приводит к потере способности восприни­мать силу P оставшимися двумя стержнями, конечно, при условии их достаточной прочности.

В заключение отметим следующие основные свойства статически неопреде­лимых систем.

1. Статически неопределимая система ввиду наличия добавочных лишних связей, по сравнению с соответствующей статически опре­делимой системой оказывается более жесткой, а при идентичном характере нагружения значения усилий получаются меньшими. Следовательно, и более экономичными.

2. Разрушение лишних связей в нагруженном состоянии, не ведет к разрушению всей системы в целом, так как удаление этих связей приводит к новой геометрически неизменяемой системе, в то время как потеря связи в статически определимой системе приводит к изменяемой системе.

3. Для расчета статически неопределимых систем необходимо предварительно задаваться геометрическими характеристиками поперечных сечений элементов, т.е. фактически их формой и размерами, так как их изменение приводит к изменению усилий в связях и новому распределению усилий во всех элементах системы.

4. При расчете статически неопределимых систем необходимо заранее выбрать материал конструкции, так как необходимо знать его модули упругости.

5. В статически неопределимых системах температурное воздействие, осадка опор, неточности изготовления и монтажа вызывают появление дополнительных усилий.

Решение статически неопределимых систем можно вести, используя три метода:

- расчет по упругой стадии деформации (допускаемым напряжениям);

- расчет по разрушающим нагрузкам;

- расчет по предельному пластическому состоянию.

В машиностроении отдается предпочтение первому методу, а в строительстве – второму и третьему.

Если в качестве физических уравнений используется закон Гука, то такой способ расчета носит название расчета по упругой стадии деформаций.После определения внутренних усилий – продольных сил в стержнях статически неопределимой системы – встает задача обеспечения ее прочности. При расчете по упругой стадии деформаций считается, что предельное состояние конструкции наступает тогда, когда один, наиболее напряженный, стержень переходит в предельное состояние (разрушится или потечет). Поэтому после определения усилий по этому способу находим напряжения в стержнях и выбираем стержень, в котором действует максимальное напряжение. Из условия прочности этого наиболее напряженного стержня либо вычисляем допускаемую нагрузку, либо подбираем сечения стержней. Следует отметить, что в большинстве статически неопределимых конструкций в результате расчета по этому способу только в одном стержне напряжения будут равны допускаемым, остальные же стержни будут недогружены. Достичь равенства напряжений во всех элементах конструкции и, следовательно, добиться выполнения требования, чтобы напряжения во всех стержнях равнялись допускаемым, в общем случае невозможно.

Второй способ расчета статически неопределимых стержневых систем носит название расчетапо предельному пластическому состоянию. Благодаря наличию лишних стержней в статически неопределимой системе, наступление состояния текучести в одном (наиболее напряженном) стержне еще не приводит к нарушению геометрической неизменяемости всей конструкции. Остальные стержни, оставаясь упругими, препятствуют пластическим деформациям этого стержня. Конструкция продолжает выполнять свое назначение, перейдя из упругой стадии работы в упругопластическую. При увеличении нагрузки в пластическую стадию работы вовлекаются все новые стержни. И только тогда, когда в системе потекут все лишние стержни и хотя бы один необходимый, конструкция превращается в механизм и не может выполнять свои функции. Это состояние и считается предельным при расчете по предельному пластическому состоянию. Таким образом, расчет по предельному пластическому состоянию сводится к следующему:

1) определяем, сколько стержней должно потечь, чтобы конструкция превратилась в механизм. Дальнейший расчет возможен по двум вариантам:

- если в предельном состоянии текут все стержни системы, то, составляя уравнения равновесия конструкции в предельном состоянии, находим из него значение предельной нагрузки ;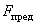

- если в предельном состоянии течет только часть стержней, то, не определяя порядка перехода стержней в пластическое состояние, рассматриваем все кинематически возможные варианты предельного состояния конструкции. Находим из уравнений равновесия предельную нагрузку для каждого варианта. Выбираем из всех вариантов минимальное значение предельной нагрузки ;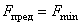

2) из условия прочности конструкции по предельному состоянию либо вычисляем допускаемую нагрузку, либо подбираем сечения стержней.

Отметим, что расчет по предельному пластическому состоянию является более экономичным, чем расчет по упругой стадии деформаций. Поэтому при сравнении результатов расчета по двум способам должно получиться, что допускаемая нагрузка, найденная расчетом по предельному пластическому состоянию, всегда не меньше нагрузки, полученной расчетом по упругой стадии деформации. Соответственно площади сечений стержней, найденные расчетом по предельному состоянию, должны быть не больше площадей сечений, полученных расчетом по упругой стадии деформаций.