Решение. Используя метод сечений, рассечем стержни и рассмотрим равновесие отсеченной части (рис.2.46, б)
Используя метод сечений, рассечем стержни и рассмотрим равновесие отсеченной части (рис.2.46, б). Составляем уравнение равновесия сил
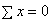 ;
; 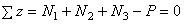 ;
;
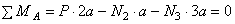 .
.
Так как неизвестных сил три, а уравнений равновесия два, система один раз статически неопределима. Для решения задачи нужно составить одно уравнение совместности перемещений.
Рассмотрим геометрическую часть задачи. Так как балка 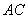 по условию задачи абсолютно жесткая, то в результате удлинения стержней она переместится вниз и повернется на некоторый угол, оставаясь прямолинейной. Положение системы после деформации стержней показано штриховыми линиями на рисунке 2.46, а.
по условию задачи абсолютно жесткая, то в результате удлинения стержней она переместится вниз и повернется на некоторый угол, оставаясь прямолинейной. Положение системы после деформации стержней показано штриховыми линиями на рисунке 2.46, а.
Составим уравнение, связывающее перемещение сечений 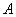 ,
, 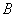 и
и 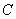 стержней
стержней
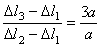 ,
,
откуда
 .
.
Используя закон Гука, выразим перемещения через силы, действующие на стержни
 или
или 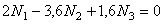 .
.
Решив полученное уравнение перемещений совместно с уравнениями равновесия, найдем
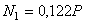 ;
;  ;
; 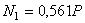 .
.
Дата добавления: 2015-08-08; просмотров: 647;
