Сила Лоренца. Известно, что на каждый элемент тока в магнитном поле действует сила Ампера:

Известно, что на каждый элемент тока 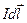в магнитном поле действует сила Ампера:

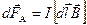. (9.9)

Если поместить в магнитное поле проводник без тока, то никакой силы мы не обнаружим. Это означает, что магнитное поле «не чувствует» неподвижные заряды. Но стоит им придти в направленное движение, в проводнике появляется ток и на проводник начинает действовать сила (9.9). Можно предположить, что магнитное поле действует на каждый отдельный носитель заряда, направленно движущийся в проводнике, а сила Ампера — интегральный результат сложения всех этих сил. Тогда силу, действующую в магнитном поле на движущийся заряд, можно вычислить, разделив силу Ампера на число носителей заряда dN, движущихся со скоростью 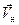на элементе проводника dl:

.

Здесь dN = n×S×dl — число носителей заряда. Вспомнив, что I = i×S, а плотность тока i = n×q×V_н, представим (9.8) в таком виде:

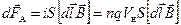. (9.10)

По определению, вектор 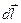совпадает по направлению с векторами плотности тока 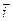и скорости направленного движения 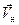. Поэтому (9.10) можно переписать ещё и так:

.

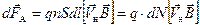Теперь, разделив эту силу на число носителей заряда dN, получим силу Лоренца — силу, действующую на заряд q, движущийся со скоростью 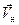в магнитном поле :

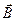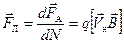. (9.11)

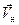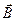Сила Лоренца пропорциональна заряду движущейся частицы q, её скорости V_н и величине индукции магнитного поля B. Кроме того, эта сила зависит от угла a между векторами и (рис. 9.2.):

F_Л = qV_нBsina.

Рис. 9.2.

В любом случае сила Лоренца перпендикулярна и вектору 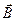и скорости движения частицы 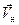. Последний результат представляет особый интерес. Если 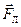^ 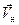, то работа такой силы всегда равна нулю:

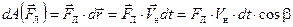=0.

Здесь b = 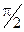— угол между векторам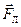и и 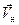; следовательно, cosb = 0 и работа 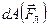= 0. Это тот случай, когда есть сила, есть перемещение точки её приложения, но работа отсутствует, благодаря особой взаимной ориентации этих двух векторов. Действие такой силы не может привести к изменению величины скорости частицы и её кинетической энергии. Действительно, согласно теореме о кинетической энергии, её изменение равно работе силы:

de_кин = dA.

Но если работа не производится, то и кинетическая энергия не меняется. Неизменность кинетической энергии означает постоянство скорости частицы.

Если заряженная частица движется со скоростью 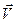одновременно в двух полях: и в магнитном и в электростатическом, то сила, действующая на неё — сила Лоренца — будет в этом случае складываться из двух сил (опять принцип суперпозиции — теперь сил!):

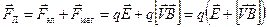. (9.12)