Теорема Гаусса и теорема о циркуляции магнитного поля. Система уравнений Максвелла электро- и магнитостатики.
Вычислив магнитное поле прямолинейного тока (8.7), мы обнаружили, что силовые линии этого поля — замкнутые окружности, охватывающие проводник с током (рис. 9.3.). Это поле можно «увидеть», разместив вокруг проводника небольшие магнитные стрелки (рис. 9.4.). Они укажут направление магнитных силовых линий в различных точках пространства.
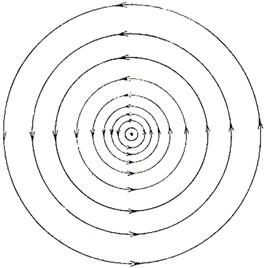
Рис. 9.3.

Рис. 9.4.
Ограниченное число магнитных стрелок можно заменить железными опилками. Каждый такой кусочек металла будет представлять собой магнитную микрострелку, которая будет ориентироваться вдоль магнитных силовых линий поля. На рис. 9.5. представлены магнитные поля кругового тока и катушки с током (соленоида), полученные с помощью таких опилок. Опилки насыпают на лист картона, пронизанный проводником с током. При постукивании по картону опилки распределяются вдоль магнитных силовых линий.

Рис. 9.5.
Присмотревшись к рисункам 9.4. и 9.5., легко обнаружить, что замкнуты не только силовые линии магнитного поля прямолинейного тока, но и силовые линии магнитных полей кругового тока и соленоида.
Можно показать, что замкнутость силовых линий магнитного поля — особенность любых магнитных полей. Здесь уместно напомнить, что силовые линии электростатического поля разомкнуты: они начинаются на положительных зарядах и заканчиваются на отрицательных. Замкнутость магнитных силовых линий приобретает принципиальное значение: из этого свойства следует вывод, что в природе нет магнитных зарядов. Электрические заряды существуют в природе. Они и являются источниками потенциальных электростатических полей. Магнитных зарядов в природе нет. Как же создаются тогда магнитные поля? Их источниками являются электрические токи. В отличие от электростатических полей, магнитные поля не потенциальные. Они называются вихревыми или соленоидальными.
Теперь обратимся к теореме Гаусса для магнитного поля. В этой теореме рассматривается поток вектора магнитной индукции через произвольную замкнутую поверхность:
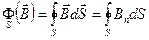 . (9.13)
. (9.13)
На рис. 9.6. замкнутая гауссова поверхность выбрана в магнитном поле прямолинейного тока.

Рис. 9.6.
Если густота магнитных силовых линий соответствует величине вектора магнитной индукции в выбранной точке пространства, то интеграл (9.12) — есть алгебраическая сумма числа силовых линий входящих (–) и покидающих (+) замкнутую поверхность. Учитывая соленоидальность магнитного поля, то есть замкнутость его силовых линий, придём к выводу: число входящих и выходящих силовых линий одинаково и их сумма всегда равна нулю:
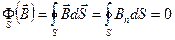 . (9.14)
. (9.14)
Полученное выражение (9.13) — математическая запись теоремы Гаусса для магнитного поля: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.
Иными словами, эта теорема утверждает: в природе нет магнитных зарядов.
Напомним, что совсем по-другому заканчивается теорема Гаусса для электростатического поля:
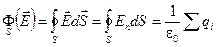 .
.
Поток вектора напряжённости электростатического поля через любую замкнутую поверхность пропорционален величине заряда, заключённого внутри этой поверхности.
Это означает, что электрические заряды — реальность природы, а вот магнитных зарядов в природе нет.
Дата добавления: 2015-08-08; просмотров: 1181;
