Магнитное поле движущегося заряда. Используя принцип суперпозиции, решим теперь задачу в некотором смысле обратную тем, которые мы решали до сих пор.

Используя принцип суперпозиции, решим теперь задачу в некотором смысле обратную тем, которые мы решали до сих пор.

В законе Био-Савара-Лапласа речь идёт о магнитном поле, создаваемом элементом тока 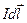. Но ведь ток — это направленное движение электрических зарядов, поэтому можно предположить, что поле элемента тока возникает как результат наложения полей, создаваемых каждым движущимся носителем заряда q₁ (рис. 8.10.).

Рис. 8.10.

Тогда поле отдельного заряда можно вычислить, разделив индукцию поля элемента тока на число носителей dN, движущихся на участке проводника dl: = .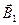

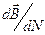Итак, запишем еще раз закон Био-Савара-Лапласа:

.

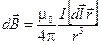Здесь I = iS, где плотность тока i = q₁×n×V_n.

Поле элемента тока перепишем ещё раз в таком виде:

.

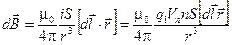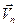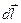Векторы и совпадают по направлению, это позволяет последнее уравнение записать так:

.

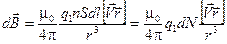Здесь dN = n×Sdl — число носителей заряда на участке dl проводника.

Искомое поле отдельного движущегося заряда:

.

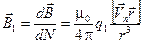Магнитное поле движущегося заряда перпендикулярно плоскости, содержащей векторы 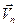и .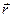

В рассмотренной задаче вектор индукции направлен на нас, нормально к плоскости рисунка (рис. 8.11.).

Рис. 8.11.

В заключение отметим, что полученный результат многократно проверен экспериментально и подтверждён для всех случаев, когда V_n << с. Здесь V_n — скорость направленного движения носителей заряда; с — скорость света.

Лекция 9 «Основы магнитостатики»

План лекции

1. Краткий обзор предыдущей лекции

2. Сила Лоренца

3. Теорема Гаусса и теорема о циркуляции магнитного поля. Система уравнений Максвелла электро- и магнитостатики.

4. Примеры расчёта магнитных полей.

4.1. Поле прямолинейного тока.

4.2. Поле бесконечного соленоида.

4.3. Поле тороида.