Магнитное поле на оси кругового тока
Теперь магнитное поле создаётся током I, протекающим по проводнику в форме окружности радиуса R. Определим магнитное поле на оси этого кругового тока в точке, отстоящей от центра круга на расстоянии r (рис. 8.9.).
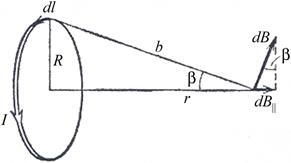
Рис. 8.9.
Вновь воспользуемся принципом суперпозиции магнитных полей. Разделим круговой ток на элементы 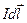 . В рассматриваемой точке на оси тока каждый такой элемент создаёт поле:
. В рассматриваемой точке на оси тока каждый такой элемент создаёт поле:
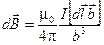 .
.
Учитывая, что векторы 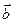 и
и 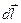 взаимно перпендикулярны, запишем модуль dB:
взаимно перпендикулярны, запишем модуль dB:
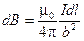 .
.
Симметрия задачи позволяет утверждать, что искомый вектор индукции будет направлен по оси кругового контура. Поэтому складывать следует осевые составляющие векторов 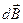 — dB||:
— dB||:
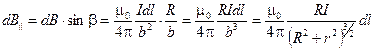 .
.
Интегрирование этого выражения по кольцу радиуса R даёт:
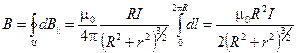 .
.
В центре контура (r = 0) индукция магнитного поля будет максимальной:
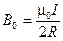 .
.
Дата добавления: 2015-08-08; просмотров: 1095;
