Краткий обзор предыдущей лекции
На прошлой лекции — первой лекции, посвящённой основам магнитостатики — был рассмотрен ряд новых физических величин, сформулированы важные законы и принципы электромагнетизма. Учитывая важность всех этих положений, сегодняшнюю лекцию начнём с их краткого повторения.
1а. Рассмотрение магнитостатики мы начали с обсуждения классических опытов Ампера. Его исследования взаимодействия параллельных токов позволили установить силу, действующую на единицу длины проводника:
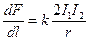 ,
, 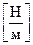 . (9.1)
. (9.1)
Этот закон был позднее использован для установления эталонной единицы электрического тока в системе СИ — одного ампера.
В уравнении (9.1) коэффициент пропорциональности k = 10–7 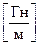 , а в рационализированной СИ k =
, а в рационализированной СИ k = 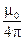 , откуда следует, что магнитная постоянная µ0 = 4p×10–7
, откуда следует, что магнитная постоянная µ0 = 4p×10–7 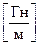 . Отметим, что µ0 в электромагнетизме является аналогом электрической постоянной e0 в электростатике (попутно заметим, что в «аналогичных» формулах магнито- и электростатики, если e0 — в знаменателе, то µ0 — непременно в числителе).
. Отметим, что µ0 в электромагнетизме является аналогом электрической постоянной e0 в электростатике (попутно заметим, что в «аналогичных» формулах магнито- и электростатики, если e0 — в знаменателе, то µ0 — непременно в числителе).
Какой закон, какая формула электростатики может быть названа «аналогом» формулы (9.1) магнетизма? Закон Кулона:
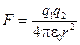 . (9.2)
. (9.2)
В уравнении (9.1) взаимодействуют два единичных элемента тока, в уравнении (9.2) — два электрических заряда.
1b. Природа силового взаимодействия токов была раскрыта в опытах Эрстеда. Было установлено, что электрический ток является источником магнитного поля, а силовое взаимодействие токов имеет электромагнитную природу.
Возникла необходимость введения количественной характеристики новой физической сущности — электромагнитного поля.
1c. Силу, с которой магнитное поле действует на проводник с током, исследовал Ампер. В законе Ампера устанавливается, что способность магнитного поля действовать на электрический ток количественно можно оценить такой векторной величиной 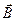 , что сила, действующая на элемент тока
, что сила, действующая на элемент тока 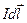 в этом магнитном поле, будет равна:
в этом магнитном поле, будет равна:
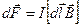 . (9.3)
. (9.3)
(9.3) — математическая запись закона Ампера.
Этот закон использован для установления единицы измерения магнитной индукции:
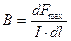 . (9.4)
. (9.4)
Вновь напрашивается аналогия с электростатикой: напряжённость электростатического поля:
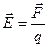 . (9.5)
. (9.5)
В качестве силовой характеристики электрического поля принята сила, действующая на единичный положительный заряд (9.5).
Силовая характеристика магнитного поля (9.4) равна силе, действующей на единичный элемент тока I×dl.
Но как связать магнитную индукцию поля 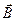 с электрическим током, который создал это поле? Ответ на этот вопрос дают два важнейших опытных положения электромагнетизма: принцип суперпозиции магнитных полей и закон Био-Савара-Лапласа.
с электрическим током, который создал это поле? Ответ на этот вопрос дают два важнейших опытных положения электромагнетизма: принцип суперпозиции магнитных полей и закон Био-Савара-Лапласа.
1d. Принцип суперпозиции утверждает, что магнитное поле, созданное произвольным электрическим током в некоторой точке пространства А, можно вычислить, сложив поля, созданные в рассматриваемой точке всеми элементами этого тока 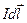 (рис. 9.1.).
(рис. 9.1.).

Рис. 9.1.
На вопрос: какое же поле создаёт элементарный элемент тока 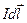 , отвечает закон Био-Савара-Лапласа:
, отвечает закон Био-Савара-Лапласа:
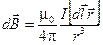 . (9.6)
. (9.6)
Вновь обратите внимание на схожесть методических подходов теорий электро- и магнитостатики.
В электростатике электрическое поле произвольной системы зарядов, на основании принципа суперпозиции, представляется векторной суммой полей точечных зарядов:
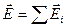 .
.
Поле точечного заряда следует из закона Кулона:
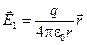 . (9.7)
. (9.7)
Сходные уравнения (9.6) и (9.7) по праву можно назвать «элементарными кирпичиками» магнитного и электрического полей (обратите ещё раз внимание на положение постоянных µ0 и e0 в этих формулах!).
1e. На этом мы завершили прошлую лекцию, проиллюстрировав рассмотренный материал расчётом магнитных полей прямолинейного тока I:
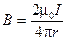 (9.8)
(9.8)
и на оси кругового тока:
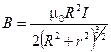 .
.
Дата добавления: 2015-08-08; просмотров: 627;
