Теорема о циркуляции магнитного поля
Теперь займёмся вычислением циркуляции вектора магнитной индукции 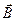 по замкнутому контуру. Начнём с простого контура. Пусть для начала контур совпадает с силовой линией магнитного поля прямолинейного тока (рис. 9.7.). По определению, циркуляция вектора по замкнутому контуру равна следующему интегралу:
по замкнутому контуру. Начнём с простого контура. Пусть для начала контур совпадает с силовой линией магнитного поля прямолинейного тока (рис. 9.7.). По определению, циркуляция вектора по замкнутому контуру равна следующему интегралу:
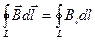 .
.

Рис. 9.7.
Обратим внимание на то, что модуль вектора магнитной индукции в нашем случае одинаков во всех точках силовой линии и, следовательно, контура L:
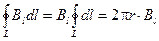 . (9.15)
. (9.15)
Согласно (9.8), 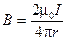 . Поэтому циркуляцию вектора
. Поэтому циркуляцию вектора 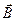 (9.15) можно записать так:
(9.15) можно записать так:
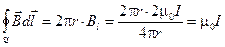 .
.
Вывод. В рассмотренном частном случае циркуляция вектора магнитной индукции по замкнутому контуру пропорциональна току, охватываемому этим контуром.
Усложним задачу. Выберем теперь почти произвольный контур L в магнитном поле прямолинейного тока I. Контур по-прежнему охватывает ток и лежит в плоскости, перпендикулярной проводнику с током (рис. 9.8.). Циркуляция 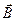 на участке контура
на участке контура 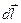 равна:
равна:
Рис. 9.8.
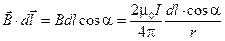
Здесь  = dj, поэтому циркуляцию по всему замкнутому контуру L можно записать так:
= dj, поэтому циркуляцию по всему замкнутому контуру L можно записать так:
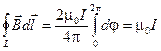 .
.
Мы вновь пришли к прежнему результату: циркуляция магнитного поля 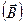 по замкнутому контуру пропорциональна току, охватываемому этим контуром.
по замкнутому контуру пропорциональна току, охватываемому этим контуром.
Что произойдёт, если контур не охватывает ток (рис. 9.9.)?
Рис. 9.9.
Циркуляция на участке 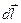 по-прежнему будет равна:
по-прежнему будет равна:
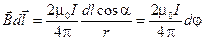 .
.
При обходе такого контура на участке 1-а-2 угол j будет расти от нуля, а на участке 2-b-1 — уменьшаться до нуля. Поэтому циркуляция в этом случае окажется равно нулю:
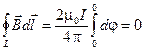 .
.
Сделаем ещё одно важное замечание. Циркуляция вектора 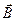 — скалярная величина. Она может быть положительной и отрицательной.
— скалярная величина. Она может быть положительной и отрицательной.
Циркуляция положительна, когда направление обхода контура связано с направлением тока правилом буравчика (рис. 9.10.a). В противном случае циркуляция отрицательна (рис. 9.10.b).

Рис. 9.10.
Если магнитное поле создаётся не одним, а несколькими токами, то циркуляция такого поля по замкнутому контуру будет пропорциональна алгебраической сумме токов, охватываемых этим контуром:
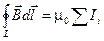 . (9.16)
. (9.16)
Для случая, представленного на рис. 9.11.:
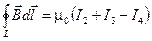 .
.
При выбранном направлении обхода контура (по часовой стрелке — на рис. 9.11.) знак тока определяется правилом буравчика. Токи I1 и I5 не вошли в сумму токов, так как они оказались вне замкнутого контура.

Рис. 9.11.
Подводя итог, сформулируем теорему о циркуляции магнитного поля: циркуляция вектора магнитной индукции по замкнутому контуру пропорциональна алгебраической сумме токов, охватываемых этим контуром.
Здесь заканчивается важный этап нашей работы: мы записали последнее уравнение системы уравнений Максвелла для электро- и магнитостатики. Вот эти уравнения:
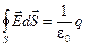 , ,
| (I) | 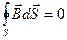 , ,
| (III) |
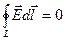 , ,
| (II) | 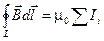 . .
| (IV) |
Система включает два уравнения потока (I и III) и два уравнения циркуляции (II и IV) для электростатических и магнитных полей.
Повторим физическое содержание этих уравнений:
| I — | источником электростатического поля являются электрические заряды; |
| II — | электростатическое поле потенциально; |
| III — | в природе отсутствуют магнитные заряды; |
| IV — | источником магнитного поля является электрический ток. |
23. Примеры расчёта магнитных полей
На ряде примеров покажем, как можно, используя теорему о циркуляции вектора магнитной индукции, рассчитать магнитные поля различных токов.
Дата добавления: 2015-08-08; просмотров: 1153;
