Действие магнитного поля на движущиеся заряженные частицы. Сила Лоренца. Магнитная индукция
На заряженную частицу, движущуюся в электромагнитном поле, действует сила, выражение для которой было получено Х. А. Лоренцем, обобщившим экспериментальные данные:
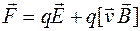 , (65.1)
, (65.1)
где  – заряд частицы;
– заряд частицы; 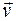 – скорость ее движения;
– скорость ее движения; 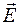 ,
, 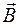 – напряженность электрического и индукция магнитного полей. Формула (65.1) является важнейшим соотношением электродинамики, так как позволяет связать уравнения электромагнитного поля с уравнениями движения заряженной частицы.
– напряженность электрического и индукция магнитного полей. Формула (65.1) является важнейшим соотношением электродинамики, так как позволяет связать уравнения электромагнитного поля с уравнениями движения заряженной частицы.
Первое слагаемое в правой части – сила, действующая на заряженную частицу со стороны электрического поля, второе – со стороны магнитного. Силой Лоренца часто называют величину
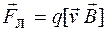 . (65.2)
. (65.2)
Так как согласно выражению (65.2) сила Лоренца пропорциональна 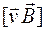 , то
, то  будет перпендикулярна
будет перпендикулярна 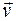 и
и 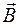 и, следовательно, не совершает работы, а лишь искривляет траекторию движения частицы, не меняя ее энергии (в отличие от электрического поля, которое ускоряет заряженную частицу).
и, следовательно, не совершает работы, а лишь искривляет траекторию движения частицы, не меняя ее энергии (в отличие от электрического поля, которое ускоряет заряженную частицу).
Проведем математическое доказательство этого факта. Уравнение движения нерелятивистской заряженной частицы в магнитном поле имеет вид
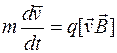 .
.
Умножим скалярно обе части уравнения на 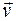 . Справа мы получим нуль, поэтому
. Справа мы получим нуль, поэтому 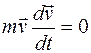 . Левую часть последнего соотношения можно представить следующим образом:
. Левую часть последнего соотношения можно представить следующим образом:
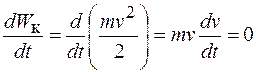 , если
, если 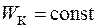 .
.
Модуль силы Лоренца определяется выражением
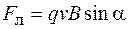 , (65.3)
, (65.3)
где 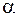 – угол между векторами
– угол между векторами 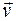 и
и 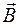 .
.
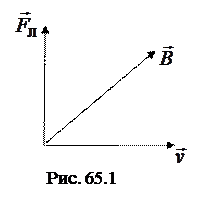 Направление вектора
Направление вектора  определяется по правилу левой руки: если четыре вытянутых пальца совпадают с направлением вектора скорости положительного заряда, линии вектора
определяется по правилу левой руки: если четыре вытянутых пальца совпадают с направлением вектора скорости положительного заряда, линии вектора 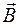 входят в ладонь, тогда отогнутый на 90º большой палец укажет направление вектора силы
входят в ладонь, тогда отогнутый на 90º большой палец укажет направление вектора силы  (рис. 65.1). Если заряд отрицательный, то используется также правило левой руки, но направление вектора
(рис. 65.1). Если заряд отрицательный, то используется также правило левой руки, но направление вектора  указывается противоположным направлению большого пальца. Векторы
указывается противоположным направлению большого пальца. Векторы  ,
, 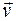 и
и 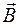 образуют правую тройку векторов.
образуют правую тройку векторов.
При  сила максимальна:
сила максимальна:
 . (65.4)
. (65.4)
Частица под действием только этой силы описывает окружность; если 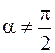 , то движение заряженной частицы происходит по винтовой линии.
, то движение заряженной частицы происходит по винтовой линии.
Согласно выражению (65.3) модуль силы 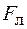 зависит не только от заряда и скорости частицы, но и от свойств магнитного поля в том месте, где в данный момент находится заряд. Силовой характеристикой магнитного поля является магнитная индукция
зависит не только от заряда и скорости частицы, но и от свойств магнитного поля в том месте, где в данный момент находится заряд. Силовой характеристикой магнитного поля является магнитная индукция 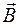 . Это векторная величина, направление которой определяется по направлению северного полюса магнитной стрелки, помещенной в данную точку магнитного поля.
. Это векторная величина, направление которой определяется по направлению северного полюса магнитной стрелки, помещенной в данную точку магнитного поля.
Магнитную индукцию можно вывести с помощью любой формулы, в которую она входит. Мы это сделаем с помощью силы Лоренца. Из выражения (65.4) получаем:
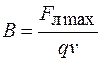 . (65.5)
. (65.5)
Согласно соотношению (65.5) можно дать определение индукции магнитного поля: магнитная индукция численно равна отношению силы, действующей на заряженную частицу со стороны магнитного поля, к произведению заряда и скорости частицы. В единицах СИ 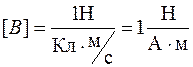 . Эта единица названа "тесла" (Тл) в честь электротехника Н. Теслы.
. Эта единица названа "тесла" (Тл) в честь электротехника Н. Теслы. 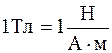 . Один тесла равен индукции однородного магнитного поля, в котором на заряд в 1 Кл, движущийся со скоростью
. Один тесла равен индукции однородного магнитного поля, в котором на заряд в 1 Кл, движущийся со скоростью  перпендикулярно полю, действует сила в 1 Н. Единица крупная, поэтому используются дольные – миллитесла (мТл) и микротесла (мкТл).
перпендикулярно полю, действует сила в 1 Н. Единица крупная, поэтому используются дольные – миллитесла (мТл) и микротесла (мкТл).
Магнитная индукция 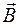 и вектор
и вектор 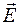 органически связаны и служат для описания электромагнитного поля. Физически это проявляется во взаимных преобразованиях полей
органически связаны и служат для описания электромагнитного поля. Физически это проявляется во взаимных преобразованиях полей 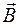 и
и 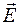 при переходе из одной инерциальной системы отсчета в другую.
при переходе из одной инерциальной системы отсчета в другую.
Для характеристики магнитного поля вводится также напряженность магнитного поля 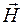 . Это векторная величина, связанная с магнитной индукцией соотношением
. Это векторная величина, связанная с магнитной индукцией соотношением
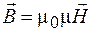 , (65.6)
, (65.6)
где 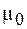 – магнитная постоянная, равная
– магнитная постоянная, равная 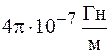 ;
; 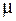 – относительная магнитная проницаемость среды.
– относительная магнитная проницаемость среды.
В единицах СИ за единицу напряженности магнитного поля принят ампер на метр 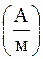 .
.
Дата добавления: 2015-08-08; просмотров: 2336;
