Вывод преобразований Лоренца

Для вывода преобразований Лоренца рассмотрим в двух системах отсчета мысленный опыт. Одна система К - неподвижна, другая К' движется вдоль оси х со скоростью V. Пусть в момент времени t = t' = 0, когда начала систем координат совпадали, в этом начале произошла вспышка света и стала распространяться сферическая световая волна. В соответствии с постулатом I фронт этой волны будет сферой в обеих системах отсчета, сфера эта будет, в соответствии с постулатом II, увеличивать свой радиус со скоростью света и в той, и в другой системе отсчета.

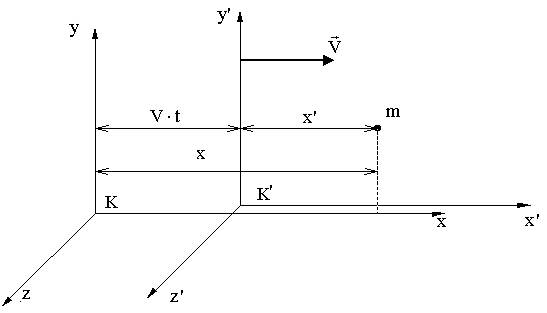
Опираясь на эти требования, найдем вид правильных преобразований координат и времени. В качестве пробного возьмем преобразование Галилея, а затем его подправим.
Фронт световой волны в системе К - это сфера радиуса ct:

x² + y² + z² = c²t²:

В системе К' уравнение фронта этой волны, в соответствии с постулатами I и II

(x')²+(y')²+(z')²=c² (t')²,

пробуем преобразования Галилея, переходим в К:

(x')² = (x - Vt)²,

(y')² = y²,

(z')² = z²,

(t')² = t²,

отсюда следует:

x² - 2Vxt + V²t² + y² + z² = c²t²,

сравните с

(x')²+(y')²+(z')² = c²(t')².

Появились ЛИШНИЕ ЧЛЕНЫ, надо так изменить преобразования, чтобы они исчезли.
Пробуем преобразования:

x' = x- Vt, y'=y, z'=z, t'=t-αx

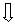
x² - 2Vxt + V²t² + y² + z² = c²t² - 2c²αxt + c²α²x²

приравниваем подчеркнутые члены, получаем:

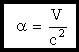
При таком α остается:

Перегруппируем члены:

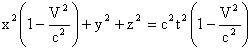
Подправим преобразование так, чтобы исчезли выражения в скобках, для этого возьмем

Такие преобразования сохраняют вид уравнения фронта световой волны, сфера преобразуется в сферу, в соответствии с постулатами С.Т.О.

Обозначим, для удобства записи,

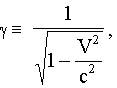
тогда преобразования Лоренца запишутся так:

а) прямые		б) обратные
;		;
;		;
;		;
;		.

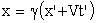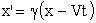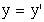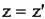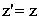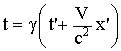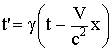Релятивистская механика должна быть построена таким образом, чтобы уравнения движения не менялись при переходе из одной инерциальной системы отсчета в другую, т.е. были инвариантны относительно преобразований Лоренца.