Элементы специальной теории относительности

8.1. Преобразования Галилея- это уравнения, связывающие координаты и время некоторого СОБЫТИЯ в двух инерциальных системах отсчета. СОБЫТИЕ определяется местом, где оно произошло (координаты x, y, z), и моментом времени t, когда произошло событие. Событие полностью определено, если заданы четыре числа: x,y,z,t - координаты события.

Пусть материальная точка m в системе отсчета К в момент времени t имела координаты x, y, z, т.е. в системе К заданы координаты события - t, х, y, z.

Найдем координаты t', x', y', z' этого события в системе отсчета К', которая движется относительно системы К равномерно и прямолинейно вдоль оси х со скоростью .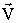

Выберем начало отсчета времени так, чтобы в момент времени t = 0 начала координат совпадали. Оси х и х' направлены вдоль одной прямой, а оси у и у', z и z' - параллельны.

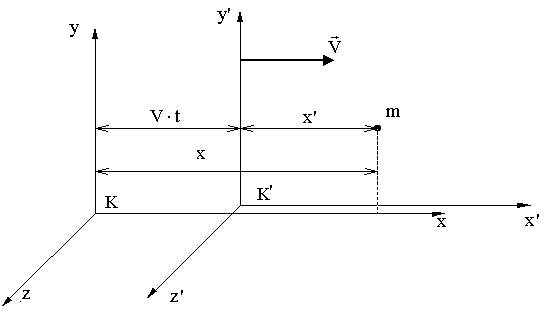
Тогда из рисунка ОЧЕВИДНО:

x = x'+Vt .

Кроме того, ясно, что для наших систем координат

y = y',
z = z'.

В механике Ньютона предполагается, что

t = t',

т.е. время течет одинаково во всех системах отсчета.
Полученные четыре формулы и есть преобразования Галилея:

x = x' + Vt,
y = y',
z = z',
t = t'.

8.2. Принцип относительности Галилея: