Лемма Лоренца. Теорема взаимности
|
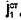 , а вторая - токами с плотностью
, а вторая - токами с плотностью 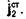 Первая группа источников создает монохроматическое электромагнитное поле
Первая группа источников создает монохроматическое электромагнитное поле 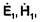 удовлетворяющее уравнениям
удовлетворяющее уравнениям
|
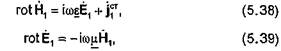
|
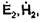 причем
причем
|
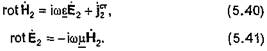
|
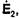 а (31) на H1, и почленно вычтем второе равенство из первого:
а (31) на H1, и почленно вычтем второе равенство из первого:
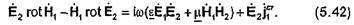
|
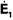 и почленно вычтем из полученного результата равенство (30), скалярно умноженное на вектор
и почленно вычтем из полученного результата равенство (30), скалярно умноженное на вектор 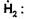
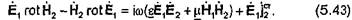
|
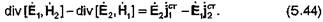
Равенство (35) называют леммой Лоренца. На основе леммы Лоренца доказывается теорема взаимности, имеющая фундаментальное значение. Предположим, что источники первой группы 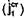 сосредоточены в конечном объеме
сосредоточены в конечном объеме 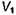 , а источники второй группы
, а источники второй группы 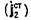 - в конечном объеме
- в конечном объеме 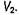 Области
Области 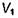 и
и 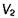 пространственно разделены (не пересекаются друг с другом).
пространственно разделены (не пересекаются друг с другом).
|
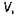 включающей в себя
включающей в себя 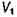 и
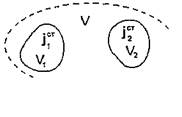
и  (рис. 49), и применяя теорему Остроградского-Гаусса, получаем
(рис. 49), и применяя теорему Остроградского-Гаусса, получаем
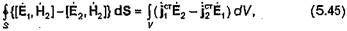
|
где S - поверхность, ограничивающая объем V.
Соотношение (46) является интегральной формулировкой леммы Лоренца.
Распространим интегрирование в уравнении (46) на все пространство. При этом поверхность S уйдет в бесконечность. Не нарушая общности рассуждений, можно считать, что амплитуды векторов 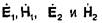 убывают с увеличением расстояния от источников быстрее, чем
убывают с увеличением расстояния от источников быстрее, чем 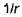 (см. теорему единственности). Тогда при
(см. теорему единственности). Тогда при 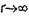 левая часть уравнения (36) обратится в нуль. Учитывая, кроме того, что по предположению вектор плотности сторонних токов
левая часть уравнения (36) обратится в нуль. Учитывая, кроме того, что по предположению вектор плотности сторонних токов 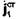 отличен от нуля только в объеме
отличен от нуля только в объеме 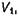 а вектор
а вектор 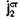 -только в объеме
-только в объеме 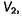 получаем
получаем
|
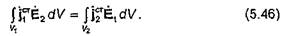
В полученном выражении 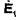 -вектор напряженности электрического поля, создаваемого в точках объема
-вектор напряженности электрического поля, создаваемого в точках объема 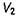 токами
токами 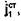 распределенными в объеме
распределенными в объеме 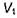 , а
, а  - напряженность электрического поля, создаваемого в точках объема
- напряженность электрического поля, создаваемого в точках объема 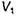 токами, протекающими в объеме
токами, протекающими в объеме 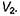
Соотношение (37) является одной из наиболее общих математических формулировок теоремы взаимности.
Выясним некоторые следствия, вытекающие из этой теоремы. Предположим, что объемы 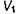 и
и 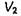 и распределение токов
и распределение токов 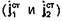 в них совершенно одинаковы. В этом случае векторы
в них совершенно одинаковы. В этом случае векторы 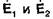 также будут одинаковыми. Например, пусть имеются две одинаковые антенны 1 и 2 с одинаковым распределением токов. Тогда вне зависимости от того, является ли разделяющее антенны пространство однородным или неоднородным, можно утверждать, что антенна 1 создает у антенны 2 такое же поле, какое антенна 2 создает у антенны 1.
также будут одинаковыми. Например, пусть имеются две одинаковые антенны 1 и 2 с одинаковым распределением токов. Тогда вне зависимости от того, является ли разделяющее антенны пространство однородным или неоднородным, можно утверждать, что антенна 1 создает у антенны 2 такое же поле, какое антенна 2 создает у антенны 1.
На основе теоремы взаимности можно также доказать, что диаграмма направленности приемной антенны имеет такую же форму, какую она имела бы, если бы антенна работала в качестве передающей. Применение теоремы взаимности в ряде случаев позволяет существенно упростить решение электродинамических задач.
При доказательстве теоремы взаимности предполагалось, что среда, заполняющая рассматриваемое пространство, является линейной и изотропной. Предположим теперь, что среда, оставаясь линейной, является анизотропной. В этом случае параметры 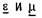 (оба или по крайней мере один из них) будут тензорами.
(оба или по крайней мере один из них) будут тензорами.
Тогда вместо уравнения (35).получаем
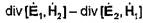
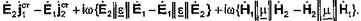
Теорема взаимности будет верна только в том случае, если выполняются равенства
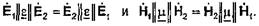
Для этого необходимо, чтобы 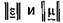 были симметричными тензорами
были симметричными тензорами 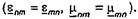 Это условие выполняется для большинства кристаллических сред. Однако в случае гиротропных сред (например, ферритов) тензор
Это условие выполняется для большинства кристаллических сред. Однако в случае гиротропных сред (например, ферритов) тензор 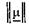 является антисимметричным
является антисимметричным 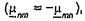 и разность
и разность 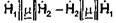 оказывается отличной от нуля. Поэтому для гиротропных сред теорема взаимности несправедлива.
оказывается отличной от нуля. Поэтому для гиротропных сред теорема взаимности несправедлива.
Дата добавления: 2015-08-14; просмотров: 1712;
