Распределение молекул по скоростям (распределение Максвелла). Распределение Гаусса. Распределение Больцмана.

Молекулы газа движутся с самыми различными скоростями, причем как величина, так и направление скорости каждой молекулы непрерывно меняется из-за соударений. Т.к. все направления движений равновероятны, распределения молекул по направлениям будет равномерным. Т.е. в пределах любым образом ориентированного, но постоянного телесного угла ∆Ω в каждый момент времени лежат в среднем одинаковое число направление скоростей молекул. Иначе дело обстоит с численными значениями скоростей молекул. Возможные значения скорости заключенные в пределах от нуля до бесконечности отнюдь не равновероятны. Изменения скоростей молекул происходит в результате соударений и, следовательно, очень малые и очень большие значения скорости маловероятны. Причем вероятность данного значения скорости стремится к нулю как при скорости, стремящейся к нулю, так и при скорости, стремящейся к бесконечности. Отсюда можно сделать вывод, что скорости молекул группируются в основном вблизи некоторого наиболее вероятного значения скорости молекул. Для выяснения способа количественного описания распределения молекул по скоростям применим следующим наглядный прием

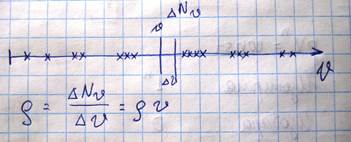
Если газ находится в равновесном состоянии, то и распределение молекул по скоростям также не будет зависеть от времени. Если имеется несколько порций одного и того же газа, находящихся при идентичных условиях(P,V,T), то распределение молекул по скоростям для них будет идентично, однако плотность изображающих точек будет отличаться и она пропорциональна рассматриваемому количеству молекул N. Но если мы введем такое соотношение

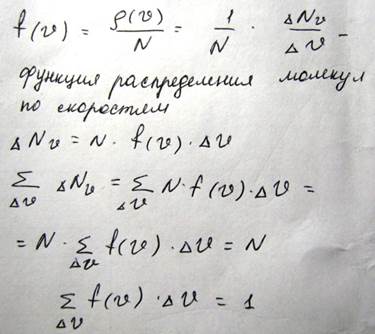
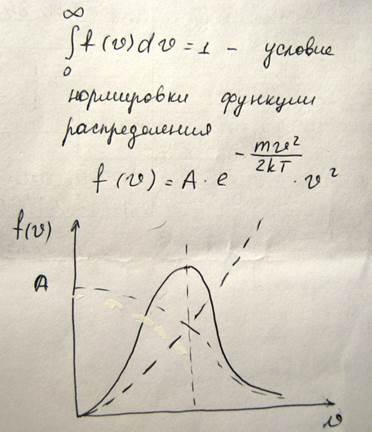
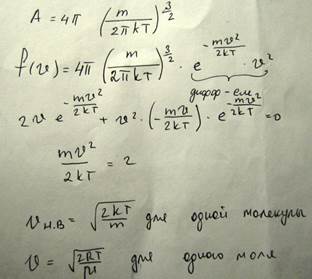
Эта формула позволяет найти количество молекул, скорости которых лежат в интервале ∆ V относительно какого-то значения скорости

Большое значение имеет средняя скорость и средняя квадратичная скорость, для описания движения молекул

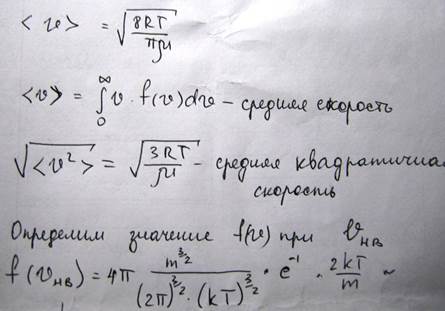
Для того чтобы найти относительное число молекул, скорость которых превышает некоторое значение V₀, нужно взять интеграл

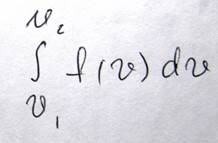
В теории случайных процессов существуют также другие функции, плотность вероятности в которых определяется множителем вида exp(-2x²). В частности к ним относится распределение Гаусса. Например, плотность вероятности отклонения пули от центра мишени на расстояние (x,y), будет равной

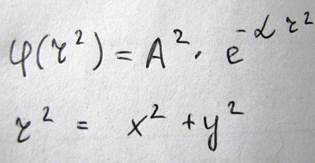
В этой формуле плотность вероятности приходится на значение r=0. Коэффициент α

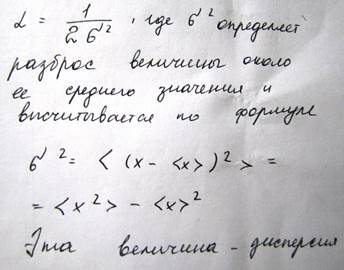
Корень квадратный из дисперсии называется стандартным отклонением или среднеквадратичным отклонением. Функция распределения Гаусса имеет след вид

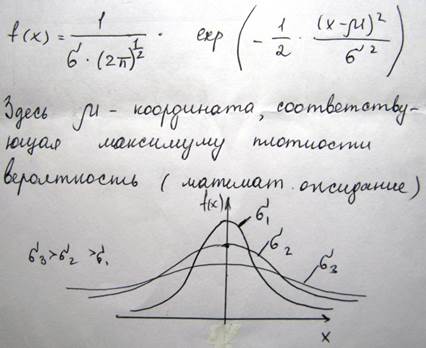
Гауссовым или нормальным распределением называется функция вида

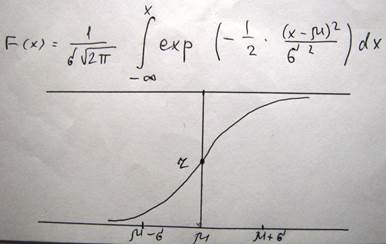
Если ввести подстановку вида

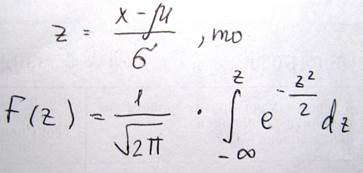
Эта функция табулирована (т.е. есть таблица).

Параметрическая формула (распределение Больцмана)

Атмосферное давление на какой-либо высоте h определяется весом вышележащих слоев газа

Распределение Больцмана показывает, как меняется концентрация молекул газа с высотой.

Модель Максвелла-Больцмана.

При рассмотрении системы многих частиц, что они обладают какими-то признаками, позволяющими отличить их друг от друга, хотя частицы и принимались совершенно одинаковыми. В связи с этим при подсчете числа микросостояний 2 микросостояния, которые отличаются тем, что две частицы поменялись своими местами, рассматривались бы как разные. Такая модель различимых частиц называется модель Максвелла-Больцмана и получающаяся при этом статистическая теория - статистикой Максвелла-Больцмана. На самом деле не известны признаки, по которым можно было бы отличить одну частицу от другой, поскольку по определению частицы принимаются совершенно одинаковыми. Если теперь взять два электрона, то их неразличимость еще более очевидна, поскольку отпадают всякие соображения о возможных различиях в их внутреннем состоянии. Если принимать частицы неразличимыми, то получаются совершенно другие правила подсчета числа микросостояний, отличающиеся от модели Максвелла-Больцмана. Статистические модели, в которых частицы принимаются неразличимыми, называются моделями Базе - Эйнштейна и Ферми - Дирака. Между собой эти модели различаются по поведению частиц в отношении микросостояний. Если в данном состоянии может находиться не более 1 частицы, то такая модель называется моделью Ферми - Дирака, а если может находиться сколько угодно частиц, то это модель Базе – Эйнштейна, при этом следует иметь в виду, что состояние характеризуется не только значением энергии, но и другими физическими параметрами. Так, например, состояния с одинаковой энергией, но с отличающимися направлениями импульса….Более точная формулировка гласит: В модели Базе - Эйнштейна в каждом квантовом состоянии может находиться любое число частиц, тогда как в модели Ферми - Дирака только одна частица. Реальные частицы являются неразличимыми и поэтому они не соответствуют модели Максвелла-Больцмана. Они подчиняются статистике либо Базе - Эйнштейна, либо Ферми - Дирака. Как было показано Паулем, частица с целым спином (фотон и фонон) описывается статистикой Базе - Эйнштейна. Частицы с полуцелым спином (электрон, протон, нейтрон, нитрин) - статистика Ферми - Дирака. В природе нет частиц, подчиняющихся статистике Максвелла - Больцмана и, тем не менее, она правильно описывает поведение частиц в очень большом числе практически важных ситуаций. Это обстоятельство связано с тем, что формулы статистик Базе – Эйнштейна и Ферми - Дирака переходят в формулы статистики Максвелла - Больцмана в том случае, когда число возможных для частиц состояний значительно больше самого числа частиц, которые могли бы занять эти состояния. Или другими словами, когда среднее число частиц приходящихся на одно состояние мало.

Явление переноса.

До сих пор рассматривался газ, находящийся в равновесном состоянии. Как известно такое состояние характеризуется одинаковостью во всех точках объема занятого газом. Теперь рассмотрим явление, возникающее при отклонении газа от равновесия. Причем ограничимся случаями, когда эти отклонения невелики. Эти явления получили название явление переноса. Рассмотрим только три таких явления: вязкость (или внутренне трение), теплопроводность и диффузия. Наука, которая изучает процессы, возникающие от равновесия, называется физическая кинетика.

Длина свободного пробега молекулы.

Молекулы газа, находясь в состоянии непрерывного хаотического движения, постоянно сталкиваются друг с другом. Минимальное расстояние, на которое сближаются молекулы при столкновении, называется эффективный диаметр молекулы

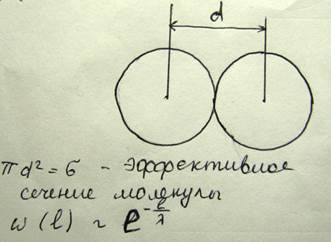
Длиной свободного пробега молекулы называется расстояние, которое проходит молекула между соударениями, вероятность того, что молекула может пройти путь l без соударения. Если в одну секунду молекула претерпевает ню соударений, то средняя длина свободного пробега λ=υ/ν. Подсчитаем среднее число соударений, которое испытывает молекула в следующей модели. Выделим одну молекулу

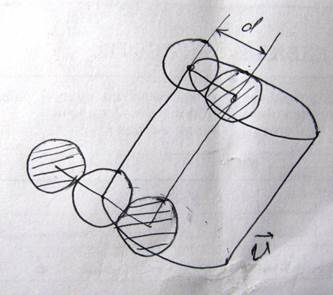
В одну секунду молекула столкнется с другими молекулами, которые находятся в цилиндре объемом ν=πd²υn. Эта формула получена в предположении, что одна молекула движется, а другие стоят. Реальное число столкновений будет больше, т.к. остальные молекулы тоже движутся и реальная длина свободного пробега определяется формулой

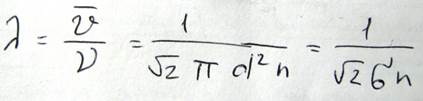
Поскольку между концентрацией и давлением существует соотношение p=nkT, можно сделать вывод, что λ~1/p. Существует также зависимость эффективного диаметра от температуры, а именно, с ростом температуры эффективный диаметр молекулы уменьшается, а длинна свободного пробега возрастает

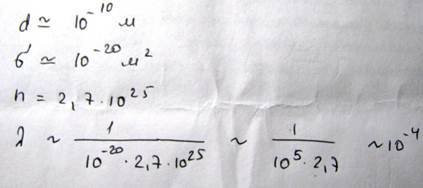
26.09.12

Вязкость газа или внутреннее трение.

Пусть мы имеем некоторый поток газа. Если скорость U в потоке газа меняется от слоя к слою, то на границе между двумя смежными слоями действует сила внутреннего трения, величина которой определяется эмпирической формулой ньютона, имеющий вид

Для выяснения природы возникновения сил внутреннего трения рассмотрим два соприкасающихся слоя

Каждая молекула газа участвует в двух движениях: хаотическом, средняя скорость которого равна V, и скорость упорядоченного движения U. |V|>>|U|. Пусть в какой-то момент времени слои обладают импульсами k₁ и k₂. Эти импульсы не могут оставаться постоянными вследствие перехода молекул из слоя в слой. За время ∆t через площадку s переходит в обоих направлениях одинаковое количество молекул, равное ∆N=(1/6)*nVS∆t. Попав в другой слой, молекула претерпевает соударение с молекулами этого слоя, в результате чего она либо отдает избыток своего импульса (если приходит из более быстрого слоя), либо увеличивает (если приходит из более медленного слоя). Пусть, например, из первого слоя за время ∆t молекулами уноситься импульс ∆K₁’=∆NmU и в этот же слой приносится ∆K₁”=∆NmU_2.

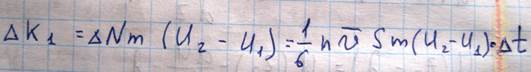
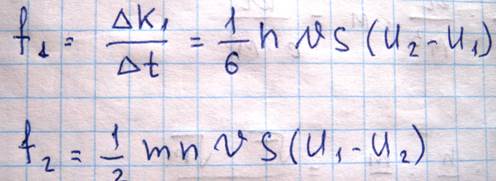
С уменьшением давления уменьшается концентрация молекул, то есть число молекул участвующих в переносе импульса между слоями. Но одновременно возрастает средняя длина свободного пробега, что свидетельствует о возрастании разницы в импульсах. Обе тенденции компенсируют друг друга. Однако этот вывод остается справедливых до тех пор, пока длина свободного пробега остается малой по сравнению с характерными размерами зазорами, по которым течет газ (диаметр трубки). Когда средняя длина свободного пробега становится сравнимой с размерами зазора, то она уже перестает зависеть от давления и определяется только размерами этого зазора. Т.к. уменьшение давления приводит к уменьшению концентрации, вязкость начинает падать. Вязкость газа меняется пропорционально корню из температуры, но на самом деле несколько быстрее, в связи с зависимостью эффективного сечения от температуры.

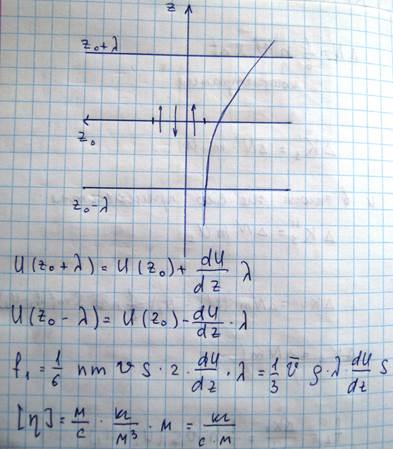
Выясним теперь как зависит коэффициент вязкости от термодинамических параметров

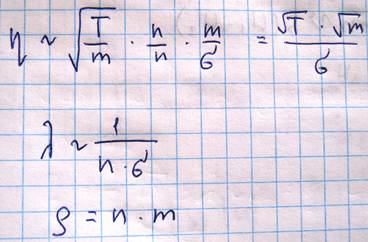
Теплопроводность

На основании многочисленных опытных данных установлены случаи, что если в какой-то среде вдоль некоторого направления z температура газа не остается постоянной, то вдоль этого направления устанавливается поток тепла, величина которого

Знак минус указывает на то, что направление, в котором возрастает температуры и направление, в котором течет тепло противоположно

Поток тепла – величина алгебраическая. Если тепло течет в положительном направлении оси z, то поток положителен, если в отрицательном, то отрицательный. Выведем выражение для количества тепла, на основе молекулярно-кинетических положений. Если температура газа в разных точках среды различна, то средняя энергия молекул также будет отлична. Перемещаясь вследствие хаотического теплового движения из одних мест в другие, молекулы переносят запасенную ими энергию. Этот перенос энергии и обуславливает процесс теплопроводности в газе. Рассмотрим газ, в котором каким-то способом поддерживается непостоянство температуры вдоль некоторого направления z (11)Количество молекул, пролетающих через площадку S в единицу времени равно

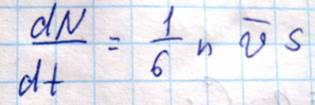
Каждая молекула несет с собой энергию, соответствующую температуре в той точке, где произошло последнее соударение с другой молекулой, а это средняя длина свободного пробега. Поэтому молекулам, летящим направо, следует приписать энергию Е₁, а молекулам справа налево – Е₂. Как известно, величины n и v зависят от температуры. Казалось бы, что для определения числа молекул, пересекающих площадку S слева направо следует подставлять n и V, соответствующие сечению 1, а справа налево значения n и V, соответствующие сечению 2. Но поскольку эти величины будут разными, то помимо переноса тепла, возникнет еще и перенос вещества. Мы будем рассматривать только перенос тепла, исключая перенос вещества. Поэтому при подсчете количества молекул, пересекающих площадку S в обоих направлениях мы возьмем для n V их значения в сечении Z₀. При этом количество теплоты, переносимого молекулами в положительном направлении оси Z будет равно

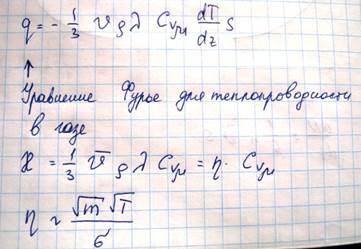
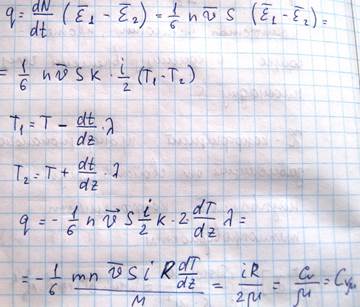
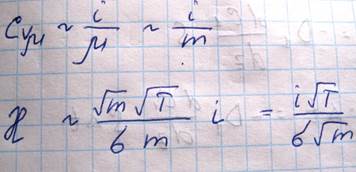
Диффузия

Рассмотрим газовую смесь, состоящую из нескольких компонентов, т.е. из молекул разного сорта. Число молекул некоторой i-той компоненты обозначим

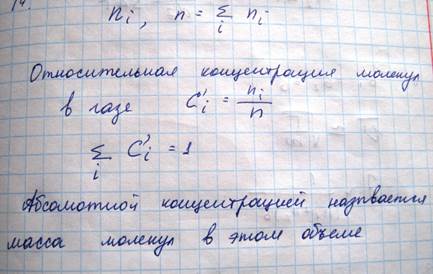
Как известно, в соответствие с законом дальтона, давление в газовой смеси равно сумме парциальных давлений газовой смеси

Может случиться так что концентрация газовых компонент в различных точках объема занимаемого этим газом будет неодинакова. В этом случае вследствие теплового движения молекул будет происходить процесс выравнивания концентраций, сопровождающийся переносом массы i-той компоненты в направлении убывания ее концентрации. Этот процесс называется диффузия. При этом полное число молекул в единице объема, а следовательно давление, в процессе диффузии не изменяется. Происходит лишь перераспределение молекул разных сортов. Т.о. возрастание концентрации какой-либо компоненты в данном месте сопровождается уменьшением концентрации в данном месте. Рассмотрим процесс диффузии с точки зрения МКТ для двухкомпонентной смеси газов. Пусть в некотором объеме каким-то образом поддерживается не изменяющийся с течением времени градиент концентрации обеих компонент вдоль направления оси Z

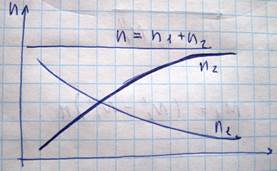
В этом случае через площадку S устанавливается преимущественный поток молекул первого сорта слева направо и молекул второго сорта справа налево. Величина массы M₁ характеризующая перенос массы первой компоненты через площадку в единицу времени имеет следующий вид

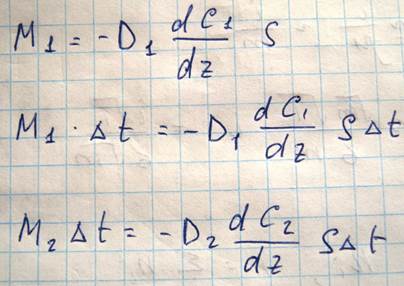
Здесь D₁-это коэффициент диффузии, dC₁/dZ - это градиент концентрации. Получим теперь выражение для коэффициента диффузии в следующей модели. Будем считать, что молекулы обеих компонент близки по массе m₁=m₂=m

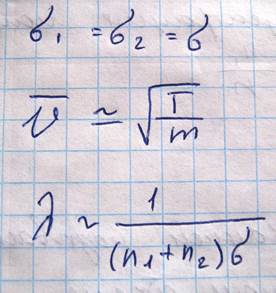
При этих допущениях молекулы обеих компонент будут иметь одинаковую длину свободного пробега. Обозначим количество молекул первой компоненты, пролетающей через площадку S в единицу времени

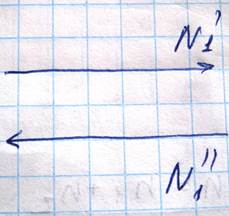
В этом случае массы молекул первой компоненты, переносимая через площадку S в направлении оси Z

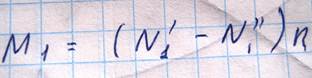
03.10.2012.

Реальные газы. Уравнение Ван-дер-Ваальса. Метастабильное состояние. Внутренняя энергия реального газа.

Уравнение Клайперона - Менделеева, которое было получено для идеального газа, описывает поведение реальных газов при не слишком высоких давлениях и не очень низких температурах.

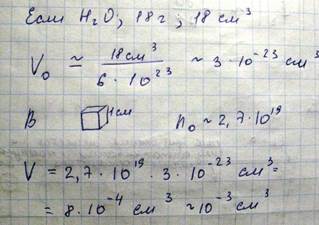
Объем занятый молекулами. Вследствие чего характер движения молекул измениться и не будет выполняться обратно - пропорциональная зависимость от объема. При сравнительно больших расстояниях между молекулами силы притяжения, называемые силами ВДВ. Эти силы возникают вследствие того что при небольшом смещении отрицательных и положительных зарядов нейтральной молекулы она превращается в диполь, т.е. совокупность двух разноименно заряженных зарядов. Этот диполь создает в пространстве вокруг электрическое поле, которое действует на другие диполи. На малых расстояниях между молекулами действуют силы отталкивания, что является просто выражением того обстоятельства, что молекула занимает некоторую область пространства и препятствует другим молекулам проникнуть в эту область. Эти силы проявляются в очень малой области порядка самой молекулы. Какой-либо универсальной формулы, описывающей потенциальное взаимодействие молекул, не существует. Однако обычно потенциальная энергия записывается в следующем виде.

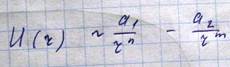
n, m выбираются из требования наилучшей аппроксимации реального потенциала

Получаемый при этом потенциал:

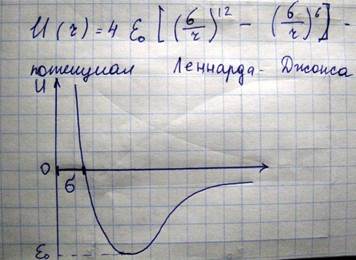
Данный потенциал является двухчастичный, т.е. сила взаимодействия между молекулами не изменяется при приближении третьей молекулы. При построении потенциальной кривой потенциальная сила равна нулю для двух молекул на бесконечном расстоянии

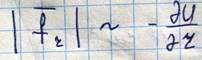
Минус обозначает, что сила взаимодействия стремиться перевести систему в состояние с минимальной потенциальной энергии. Рассмотрим с помощью этой кривой процесс столкновения двух молекул.

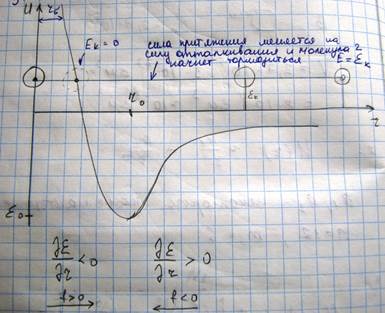
Поместим мысленно в центр одной молекулы начало координат. Вторая - на бесконечности, обладает некоторым запасом кинетической энергии. Вторая молекула будет разгоняться (с ускорением), так что полная энергия останется такой же, так как система из двух молекул замкнута. В той точке, где полная энергия будет равна потенциальной энергии, молекула остановится. Это минимальное расстояние, на которое могут подойти молекулы друг к другу. Эта кривая демонстрирует факт уменьшения эффективного диаметра молекулы при повышении температуры. В случае идеального газа потенциальная кривая имеет такой вид

Поведение реальных газов точнее всего описывается уравнение ВДВ, которое имеет следующий вид

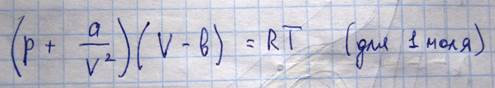
Оно является вириальным уравнением, так как оно может быть представлено

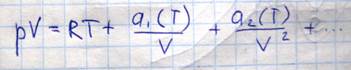
Преобразуем уравнение Ван-дер-Ваальса:

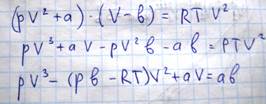
B учитывает то пространство, которое молекулы не могут занимать, т.к. они обладают объемом

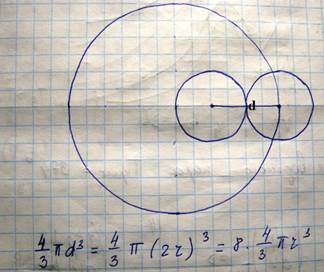
Из этого рисунка видно, что центры двух молекул не могут занять объем радиусом d. Добавочное давление связано с …если бы между молекулами исчезла бы сила взаимодействия, то для того чтобы удержать молекулы в прежнем объеме, понадобилось бы добавочное давление, которое вычисляется

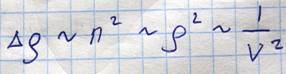
Все корни вещественны, либо один - вещественный, а два остальных комплексно сопряженные. Поскольку V является физическая величина, то выбирается вид с тремя вещественными решениями. Графическое решение

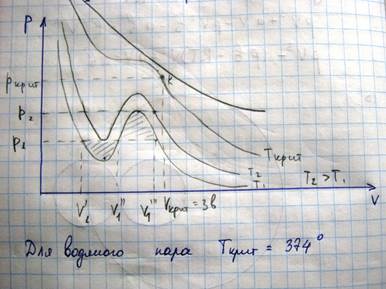
Касательная к критической изотерме в точке К является пределом, которому стремятся секущие р1,р2… Следовательно, также как и они проходят оси объему

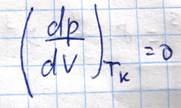
Кроме того, поскольку К – это точка перегиба

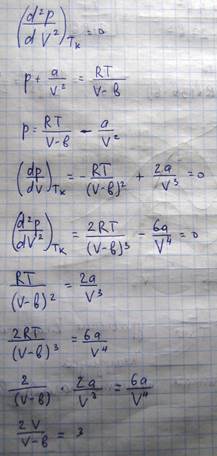
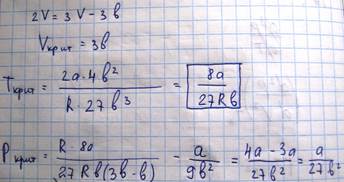
Экспериментальные изотермы ВДВ.

При уменьшении объема газа давление будет нарастать, однако при достижении значения V_г наблюдается отклонение от теоретического давления, а само вещество перестает быть однородным.

Наблюдает неоднородное двух фазное состояние вещества. При состоянии, соответствующему горизонтальному участку изотермы, наблюдается равновесие между жидкой и газообразной фазами вещества. Газ, находящийся в равновесии со своей жидкостью, называется насыщенным паром. В области двухфазного состояния, при котором вещество находится в равновесном состоянии

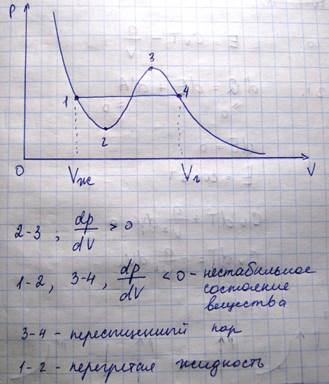
Тот факт, что вместо S-образной кривой наблюдается 1-4 связан с неустойчивостью однофазных состояний в траектории 1-2-3-4.

Внутренняя энергия реального газа

Взаимодействие между молекулами реального газа обуславливает их взаимную потенциальную энергию, которая входит во внутреннюю энергию газа, наряду с кинетической энергией

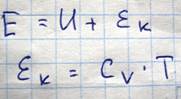
Потенциальная энергия взаимодействия молекул газа проявляется при совершении работы против сил притяжения молекул в процессе расширения газа и равна

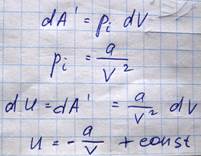
Значение константы в этом выражении выбирается из того факта, что при V->бесконечности, выражение для внутренней энергии реального газа должна описывается как и внутренняя энергия идеального газа + добавка

Внутренняя энергия реального газа возрастает как при росте температуры, так и при росте давление?. Если теперь мы производим расширение или сжатие реального газа без теплообмена с окружающей средой и без совершения внешней работы, то 1 начало термодинамики, приводит к тому, что dE=0, значит E=const

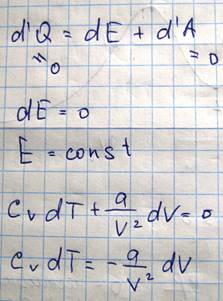
Откуда следует, что если dT>0, то dV<0 и наоборот.

Циклические процессы, или круговые процессы.

Основные термодинамические процессы, т.е. процессы изменения состояния идеального газа (изотерма, изобара, изохора, адиабата) на диаграмме p-V изображается отрезками кривых или прямых, из которых видно, что в начальной и конечной точке данного процесса система находится в различных состояниях.

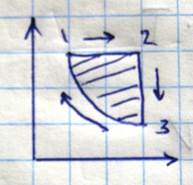
Однако большое значение имеют такие процессы, когда система в конце приходит в исходное состояние и параметры принимают первоначальное значение. Эти процессы называются циклическими процессами

10.10.12

Циклы, в которых работа совершается за счет затраты теплоты, называется прямыми циклами. В этих циклах линия расширения газа лежит выше линии сжатия газа на диаграмме P-V. Прямые циклы совершают все тепловые машины (паровые и Двигатели внутреннего сгорания). Обратные циклы – циклы, на осуществление которых расходуется механическая энергия. По обратному циклу работают все холодильные машины. Наиболее экономичный, т.е. обладающий наибольшим кпд, является цикл Карно

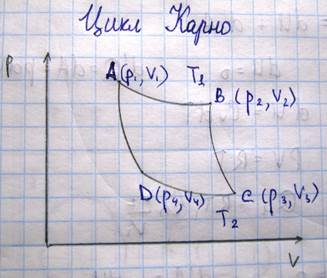
Для практического осуществления цикла Карно необходимо наличие рабочего тела (цилиндр с газом под поршнем, и два термостата)

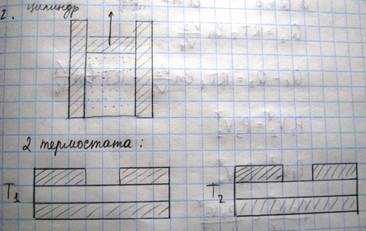
Термостаты обладают бесконечно большой теплоемкостью. Термостат №1, который будет сообщать тепло-нагреватель, термостат №2-холодильник. Пусть сначала рабочее тело расширяется по изотерме АВ, характеризуемый температурой Т₁. Цилиндр ставим в термостат 1, нагревается, газ расширяется и совершает работу против внешней силы, работа равна площади под кривой АВ, рабочему телу сообщим кол-во теплоты Q₁. Если бы расширение газа при этом осуществлялось не бесконечно медленно, то темп газа упала бы ниже температуры нагревателя Т₁, т.к. не успевало бы происходить теплопередача от термостата к цилиндру. Для того, чтобы процесс расширения газа был обратимым, необходимо увеличивать его объем бесконечно медленно. По достижении точки В цилиндр снимается с термостата и его дно закрывается теплоизолирующей крышкой, газ за счет внутренней энергии будет расширяться, причем процесс будет адиабатическим. При этом температура газа упадет и давление также понизится. Приходим в точку С, у газа температура Т₂, ставим цилиндр на холодильник. Начинаем сжимать газ, уменьшается объем, возрастает давление. При этом газ отдает холодильнику количество теплоты Q₂, работа совершается А₂ (работа внешних сил). Достигнув точки D, дно закрываем теплоизолятором, продолжаем процесс сжатия газа. Приходим в точку А. Цикл совершен. Раб тело получает от нагревателя при расширении по изотерме АВ количество теплоты Q₁, а при сжатии по изотере СD рабочее тело отдает холодильнику количество теплоты Q₂. При изменении состояния газа по адиабатам BC DA рабочее тело не получает и не отдает теплоты. Т.о. в результате совершения цикла рабочее тело совершает работу эквивалентную Q₁-Q₂

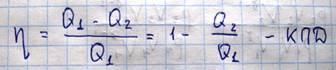
Поскольку изотермический и адиабатический процессы, входящие в цикл Карно являются обратимыми процессами, то и весь цикл является обратимым. Посчитаем кпд цикла Карно, если под поршнем будет находиться идеальный газ

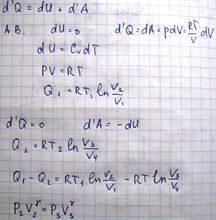
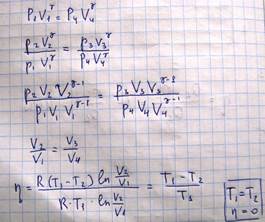
Из этого выражения видно, что если Т₁=Т₂, то кпд будет равен 0. Нельзя затратить теплоту, совершить работу, если все тела системы находятся при одинаковой температуре. На практике двигатели внутреннего сгорания и тепловые машины не работают по циклу Карно, поскольку не удается осуществить изотермические процессы. Более того, осуществляемые в тепловых машинах циклы необратимы и в действительности даже не замкнуты, т.к. в них рабочая смесь, т.е. сгоревшая смесь газов по окончании циклов выбрасываются наружу.

Второе начало термодинамики

Первое начало термодинамики позволяет решать многие термодинамические задачи, но совершенно не рассматривает вопрос о направлении происходящих процессов. Первому началу термодинамики не противоречит такая ситуация (сколько кол-во теплоты первое тело отдает, столько же должно получить второе тело)

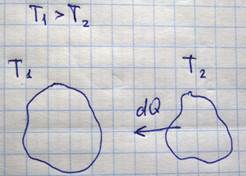
Второе начало термодинамики устанавливает направление термодинамических процессов. Существует несколько эквивалентных формулировок второго начала термодинамики:

Постулат Клаузиуса: Теплота не может сама собой перейти от тела менее нагретого, к телу, более нагретому без одновременных изменений в самих телах или в окружающей среде.

Постулат Томсона: невозможно построить такую периодически действующую круговую машину, которая непрерывно бы совершала работу за счет теплоты, выделяемой системой при охлаждении, причем никаких других изменений в этой системе или окружающей среде не происходило бы.

Постулат без имени: Невозможно осуществить вечный двигатель второго рода, такой периодически действующий двигатель, т.к. такой который получал от одного резервуара и полностью превращал бы его в работу

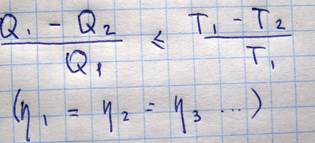
Теорема Карно.

Из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателя и холодильника, наибольшим кпд обладают обратимые машины. При этом КПД таких машин равны друг другу и не зависят от конструкции машины. Из теоремы Карно можно получиться эквивалентные формулировки второго начала термодинамики. Пусть теплота переходит от одного тела к другому без совершения работы Q₁=Q₂, A=0

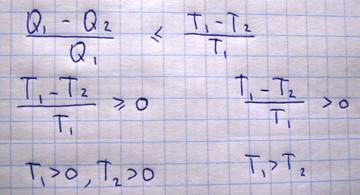
Поскольку процесс передачи тепла является необратимым, то в этом выражении знак равенства убирается и остается лишь больше (>). Одна из формулировок второго начала термодинамики утверждает, что невозможно построить вечный двигатель второго рода, т.е. нельзя того, чтобы вся теплота полученной системой превращалась в работу

Следовательно, вечный двигатель второго рода можно было бы построить при обязательном выполнении двух условий: 1)Цикл работы машины должен быть обратим, т.к. стоит знак равенства; 2) Температура холодильника должна быть равна нулю Кельвина.

Энтропия.

Количество теплоты получаемой системой d’U и работу d’A совершенной системой нельзя выразить как полные дифференциалы параметров описывающих состояние данной системы

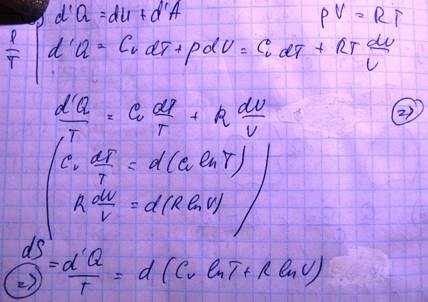
Выражение, стоящее в правой части, представляет собой полный дифференциал, следовательно, в левой части тоже полный дифференциал. S - энтропия. Выражение называется приведенная теплота. T – интегрирующий множитель для d’Q. [S]= Дж/К

Энтропия является экстенсивной величиной, т.е. ее величина зависит от массы вещества. Энтропия является аддитивной величиной, т.е. энтропия сложной системы равна сумме энтропий отдельных ее частей

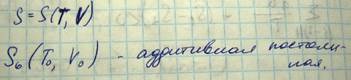
Энтропия является функцией с точностью до аддитивной постоянной в качестве которой можно взять некое S₀(T₀,V₀). Начальное значение энтропия определяется третьим законом термодинамики или теоремой Нернста: Энтропия системы стремиться к нулю при стремлении к нулю температуры системы

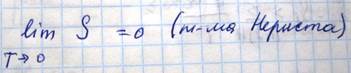
Энтропия системы является однозначной функцией состояния системы и поэтому она может служить таким же параметром системы, как и температура, давление и объем, однако в отличие от них она не может быть посредственно измерена и функциональная связь определяется из уравнения

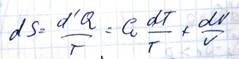
Если имеет место обратимый круговой процесс в результате, которого система возвращается к исходному состоянию, то изменение энтропии в этом случае будет равно нулю

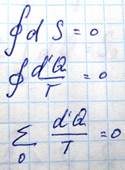
В случае если процесс необратим, то для него

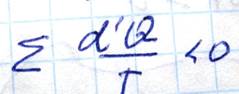
Поскольку необратимые процессы всегда сопровождаются потерями тепла. Теперь найдем изменение энтропии при необратимом процессе

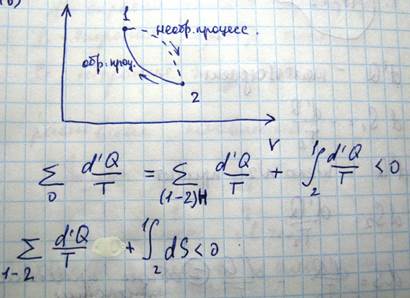
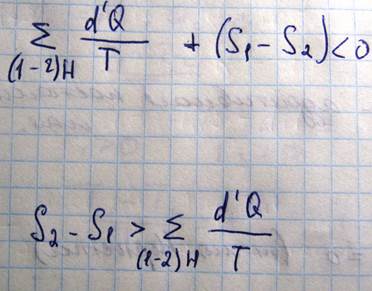
Если система изолирована, т.е. она в целом не получает и не отдает теплоты, то d’Q=0 и отсюда получается, что ∆S=S₂-S₁>0. В изолированных системах могут происходить только такие процессы, при которых энтропия системы не уменьшается, и в частности при необратимых процессах энтропия возрастает, в случае же обратимых процессов энтропия не изменяется. Если система находится в состоянии с максимальной энтропией соответствующей ее энергии, то в ней не могут происходить никакие другие процессы, поскольку любой процесс будет сопровождаться уменьшением энтропии. Это означает, что состояние с максимальной энтропией является наиболее устойчивым состоянием изолированной системы

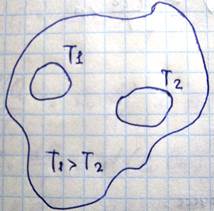
Самопроизвольно теплообмен между этими телами будет происходить таким образом, что с течением времени их температура станет одинаковой, этот процесс является необратимым процессом. Пусть первое тело за малый промежуток времени количество теплоты отдаст d’Q

Таким образом, при теплообмене энтропия системы возрастает, причем неважно каким образом происходить процесс теплопередачи либо путем излучение или путем теплопроводности. С введением понятия энтропии одна из формулировок второго начала термодинамики о самопроизвольной передаче тепла от более нагретого тела к менее нагретому телу формулируется как закон возрастания энтропии: в изолированной системе изменение энтропии при любом процессе должно удовлетворять равенству dS=>0 , и с учетом математического выражения для первого начала термодинамики закон возрастания энтропии

Подсчитаем теперь изменение энтропии при изотермическом обратимом процессе

Этим уравнением описывается равновесие жидкости с ее паром при неизменной температуре. Подсчитаем работу совершенной системой при изотермическом обратимом процессе (воспользуемся первым началом термодинамики)

Свободная энергии это часть внутренней энергии, которая может быть превращена в работу при изотермическом обратимом процессе. Величина TS это так называемая связанная энергия F=U-TS.

17.10.12

Можно определить изменение энтропии идеального газа

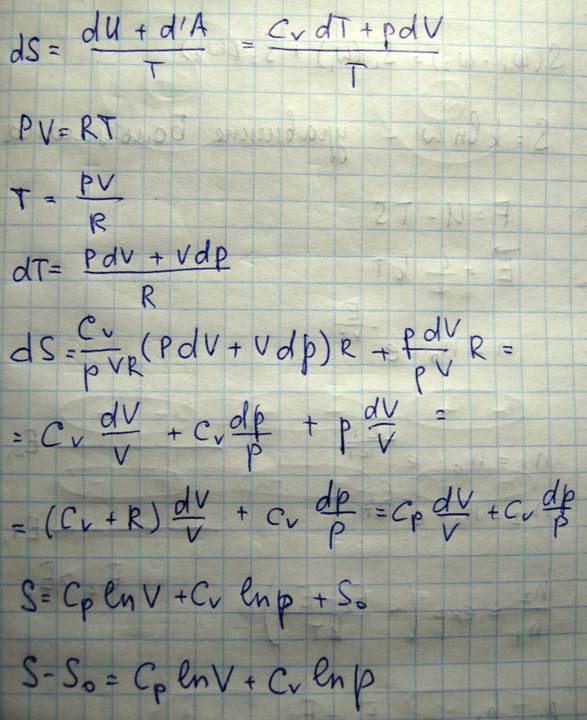
Процесс самопроизвольного выравнивания температур двух тел, первоначально имеющих различные температуры, является необратимым, потому что начальное состояние системы менее вероятно, чем состояние, при котором энергия молекул более равномерна, распределена между обоими телами. Таким образом, всякий необратимый процесс это такой процесс обратный которому крайне маловероятен. Необратимые процессы, как было ранее показано dS=>0, сопровождаются возрастанием энтропии и когда энтропия достигает максимального значения, то система приходит в равновесное состояние являющееся наиболее вероятным. Таким образом, статистическая причина возрастания энтропии при необратимых процессах состоит в увеличении при этом вероятности состояния системы. Следовательно, сама энтропия системы есть некоторая функция вероятности состояния системы. Это положение впервые было выдвинуто Больцманом:

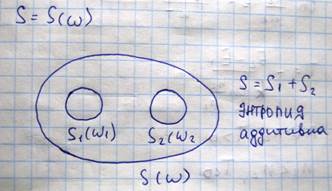
Из теории вероятности следует:

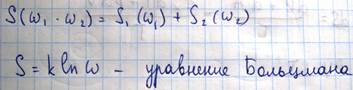
Таким образом, соотношение Больцмана позволяет энтропии статистическое толкование, то есть энтропия есть мера неупорядоченности системы, чем больше неупорядоченность системы, тем больше ее энтропия. Например: пусть исходное состояние система газ, при конденсации газа энтропия системы убывает, так как в процессе конденсации молекулы, они будут располагаться более упорядоченно, еще большее убывание энтропии будет происходить при кристаллизации жидкости и наконец, при абсолютном нуле температуры всякое тепловое движение прекращается всякое неупорядоченность исчезает и энтропия обращается в ноль, учитывая, что в замкнутых системах необратимые процессы сопровождаются возрастанием энтропии и полагая, что наша вселенная является замкнутой системой, немецкий физик Клаузиус высказал в конце 19 века мысль о «тепловой смерти» вселенной, так как он рассуждал: Рост энтропии означает рост связанной, то есть обесцененной энергии TS в уравнении F=U-TS, которая не может быть использована для совершения работы, следовательно, все виды движения во вселенной должны самопроизвольно перейти в тепловое хаотическое движение, температуры всех тел во вселенной должны выровняться и наступит «тепловая смерть». И в заключение темы об энтропии, рассмотрим понятие об отрицательной абсолютной температуре. Абсолютная температура в молекулярно-кинетической теории определяется как величина пропорциональная средней кинетической энергии, поскольку кинетическая энергия величина положительная то, отсюда следует, что и абсолютная температура так же положительная величина, однако если воспользоваться распределением Больцмана:

можно получить более общее определение понятия абсолютной температуры

В равновесном состоянии n₁>n₂, т.е. T>0 , если n₁<n₂, то T<0

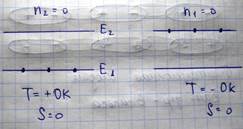
Однако с точки зрения энергии эти состояния различны. Состояние с отрицательной температурой ответствует инверсной заселенности. Состояние систем микрочастиц (электронов) характеризуемые отрицательной температурой, используется при создании квантовых усилителей и генераторов электромагнитных волн (квазаров, лазеров).