Канонический ансамбль. Распределение Гиббса. Статистическая сумма.
Рассмотрим скоростные и энергетические состояния, которые представляют изучаемую в данном случае систему. Но эта система уже теперь не замкнута. Поскольку она обменивается энергией с другими частицами, составляющими вместе с ней замкнутую систему.
Совокупность незамкнутых статистических систем называется каноническим ансамблем.
Отдельная система канонического ансамбля может содержать как одну, так и много частиц. Важным является только то, чтобы число ее частиц было значительно меньше числа частиц большой системы. Энергия различных систем канонического ансамбля различна. И проблема заключается в определении вероятности различных энергетических состояний систем этого ансамбля. Согласно распределению Гиббса или канонического распределения вероятность того, что система находится в состоянии с энергией εа:
Pa=A*e- βεа ,
β=1/kT,
A=Гα0 / Г0 ,
где Г0 - это число состояний, принадлежащих микроканоническому ансамблю, а Гα0 - число микросостояний полной системы, посредством которых осуществляется состояние с нулевой энергией у рассматриваемой канонической подсистемы. Распределение Гиббса может быть также записано через статистическую сумму
Pa=(e- βεа )/(∑a e- βεа)
Статистическая сумма представляет собой функцию всех микросостояний одновременно.
Основное уравнение молекулярно-кинетической теории газа (для давления)
Давление газа на стенки сосуда возникают вследствие ударов молекул. Молекулы движутся совершенно беспорядочно. Все направления движений равновероятны. Основанием для такого утверждения служит тот опытный факт, что давление газа на стенки сосуда всюду одинаков. Для математического упрощения решения задачи о вычисления давления примем два допущения:
1) Молекулы движутся вдоль трех взаимно перпендикулярных направлениях.
2) Все молекулы имеют одинаковое значение скорости.
Выделим в газе площадку площадью дельта S, положение которой будет задано внешней нормалью n. (3) За время дельта t до элемента дельта S долетят все молекулы, которые находятся в цилиндре с площадью основания ∆S и высотой v*∆t.
1/6n*v*∆t*∆S=N
∆k=2mv*1/6n*v*∆t*∆S=1/3nmv2∆S
∆F=∆k/∆t=1/3 nmv2∆S
P=∆F/∆S=1/3 nmv2=2/3nε
Данное выражение получено в предположении, что все молекулы движутся с одинаковой скоростью. Учет того факта, что молекулы движутся с разными скоростями, что давление равно
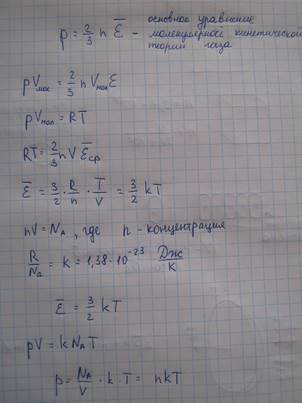
Если при данной температуре имеется смесь различных газов, то разные по массе молекулы будут иметь различную среднюю скорость, но средняя энергия молекул будет одинаковой. Полное давление в этом случае будет равно
p = nkT = (n1+n2+…+ni)kT= n1kT+n2kT+nikT
Это закон Дальтона: давление в смеси газов равно сумме парциальных давлений газов, образующих данную смесь.
Воздух: 77% N2 + 20% O2

Это уравнение учитывает только энергию поступательного движения молекул. Однако возможно также вращение молекулы и колебание атомов, входящих в состав молекулы. Естественно, что эти оба вида движения также связаны с определенным запасом энергии, вычислить которые позволяет устанавливаемое статистической физикой положение о равнораспределении энергии по степеням свободы молекулы. Числом степеней свободы механической системы является число независимых величин, с помощью которых может быть задано положение системы. Материальная точка, например, имеет три степени свободы. Для того чтобы перейти от материальной точки к твердому телу необходимо ввести понятие центр инерции. Центр инерции твердого тела – это такая материальная точка, которая обладает массой этого тела и которая движется под действием сил действующих на тело так, как движется само тело. Абсолютно твердое тело обладает шестью степенями свободы.
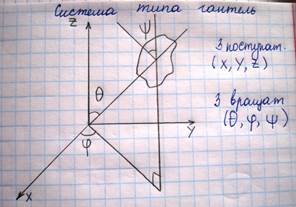
Если положение атома, входящих в составе молекулы не фикс, то добавляется степень свободы колебания. Нужно иметь ввиду, что колебательная степень свободы обладает вдвое большей энергетической емкостью по сравнению с поступательной или вращательной. Это связано с тем, что при колебаниях изменяется как кинетическая, так и потенциальная энергия, средние значения которых равны.
i=nпост+nвращ+2nкол
Внутренняя энергия идеального газа
Поскольку молекулы идеального газа не взаимодействуют между собой на расстоянии, то внутренняя энергия системы будет складываться из энергий отдельных молекул
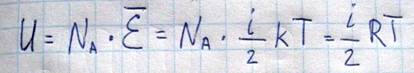
Теплоемкость – это физическая величина, равная количеству теплоты, которое необходимо сообщить телу для того, чтобы увеличить его температуру на один градус(К).
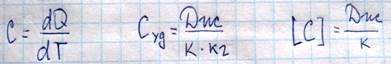
Помимо этого в молекулярной физике вводится теплоемкость при постоянном объеме и при постоянном давлении, в зависимости от того, при каких условиях к системе подводится тепло. Если нагревание происходит при постоянном объеме, то система не совершает работы над внешними телами и все тепло, которое сообщается системе, идет на изменение внутренней энергии.
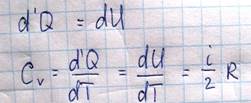
В том случае, если нагревание происходит при постоянном давлении, то газ может расширяться и совершать работу над внешними телами
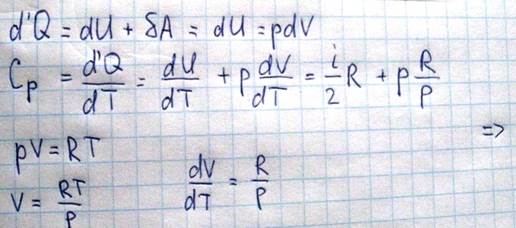
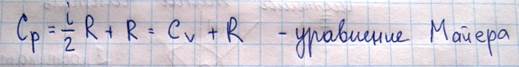
Используя уравнение Майера можно вычислить
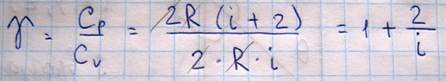
Уравнение адиабаты идеального газа
Адиабатическим называется процесс изменения состояния идеального газа происходящий без теплообмена с окружающей средой. Для адиабатического процесса:
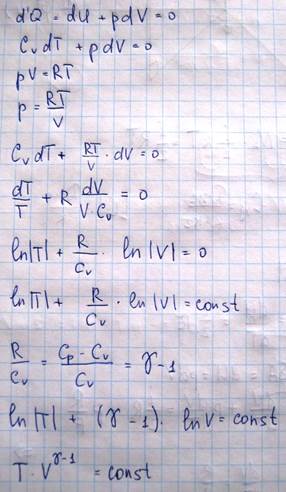
Реально адиабатическими процессами могут быть только быстро протекающие процессы, поскольку в природе не существует вещества совершенно не проводящего тепло. Пример адиабатического процесса - взрыв. Процессы изменения состояния идеального газа относятся к политропическим процессам, поскольку все (изопроцессы) они могут быть математически представлены в виде соотношения
pVn=const
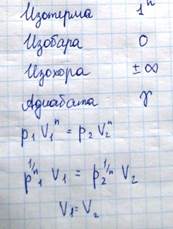
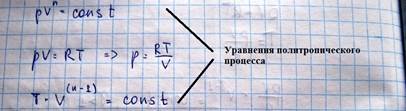
Найдем выражение для теплоемкости политропического процесса:
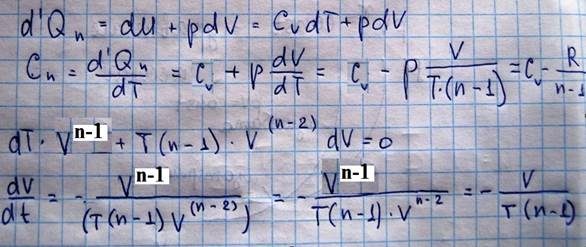
При политропическом процессе теплоемкость газа остается постоянной, то есть она не зависит от параметров состояния P,V,T.
19.09.2012
Дата добавления: 2015-08-08; просмотров: 2272;
