Строение кристаллов
Идеальный кристалл можно представить себе как тело, полученное в результате построения путем бесконечных повторений идентичных структурных элементов (кирпичиков). Простейших монокристаллов кирпичиками является одинаковые атомы, но в большинстве случаев кирпичик состоит из нескольких атомов или молекул, причем их число может быть достаточно велико. Идеальный кристалл это есть тело состоящее из атомов расположенных в пространственной решетке и всегда можно выделить три вектора элементарных смещений (трансляций) a,b,c обладающих тем свойством что атомное расположение имеет одинаковый вид как из некоторой точки заданной радиус вектором р
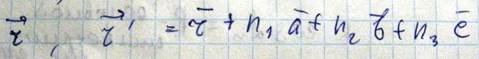
Операция перемещения кристалла параллельно самому себе описываемый вектором называется трансляцией
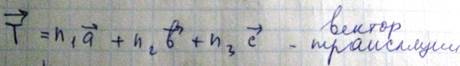
Векторы смещения a, b, c обычно выбирается в качестве ортов системы координат, наиболее отличительной чертой кристаллической структуры является наличие операции симметрии то есть таких операций в результате которых кристалл переходит сам в себя. Параллелепипед образованный векторами смещения a, b, c называется примитивной ячейкой
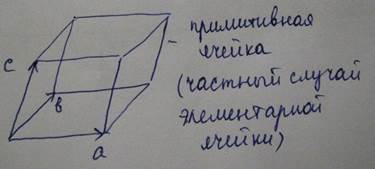
Примитивная ячейка является частным случаем элементарной ячейки. Элементарная ячейка это любая ячейка, обладающая тем свойством, что применение к ней операций трансляций являющихся операцией симметрии для кристалла заполняет все пространство. Примитивная ячейка это элементарная ячейка наименьшего объема. Её можно выбрать так чтобы во всех углах соответствующего ей параллелепипеда находились бы только точки решетки. Как известно векторная алгебра дает такое соотношения для параллелепипеда
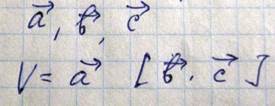
В случае если a, b, c вектора трансляции, то V объем элементарной ячейки. Помимо трансляции кристаллические структуры часто характеризуются также такими операциями симметрии как повороты вокруг осей проходящих, например через одну из точек решетки. Существуют решетки обладающие осями первого, второго, третьего, четвертого и шестого разрядов
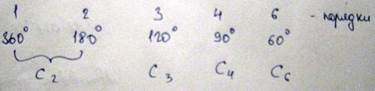
Других типов осей симметрии, то есть поворотов вокруг которых превратил бы кристалл в самого себя, не существует. Рассмотрим процесс размножения поворотной оси симметрии порядка Cn

Иллюстрацию этой теоремы можно легко найти в рисунках паркетах. Сплошное покрытие плоскости одинаковыми и параллельными многоугольниками возможно только ровными прямоугольниками, квадратами, шестиугольниками, ромбами. Рассмотрим теперь характеристики наиболее простых пространственных решеток относящихся к кубической сингонии
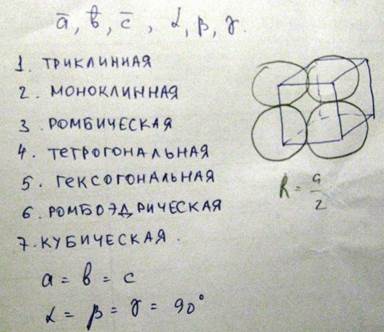
| Характеристика | p | F | I |
| Объем элементарной ячейки | а3 | а3 | а3 |
| Количество атомов в ячейке | |||
| Расстояние между ближайшими соседями | а | (а√2)/2 | (а√3)/2 |
| Число ближайших соседей (координационное число) |
Число ближайших соседей, реализуемое для гранецентрированного куба, является максимально возможно
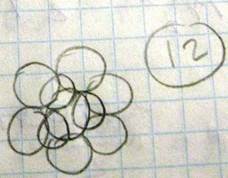
31.10.2012
Упругие и тепловые свойства твердых тел.
Наиболее характерными физическими свойствами, которыми обладают твердые тела, являются их механические свойства – прочность, твердость, пластичность, обусловленные упругими характеристиками кристаллов. При действии на кристалл внешней растягивающей нагрузки, расстояние между атомами увеличивается, и равновесное положение их в кристалле нарушается. Это приводит к нарушению равенства сил отталкивания и притяжения и к возникновению сил стремящихся вернуть атомы в первоначальное положение равновесия. Величина этих сил отнесенная к единице площади поперечного сечения кристалла называется напряжение (сигма). Как известно потенциальная энергия взаимодействия двух частиц в твердом теле описывается
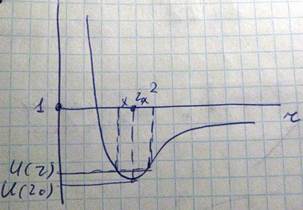
При смещении атома номер 2 потенциальная энергия меняется и приобретает значение U(r). Изменение потенциальной энергии системы равно
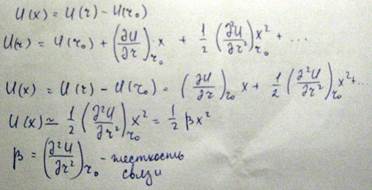
Учитывая в разложении потенциальной энергии члены до 2 порядка мы аппроксимируем потенциальную энергию параболической зависимостью
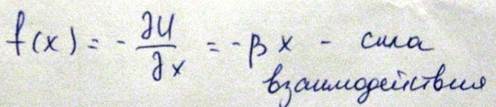
Из этого выражения видно, что сила пропорциональна смещению частиц от положения равновесия и направлена в сторону равновесия, что указывается знаком минус. Известно, что под действием такой силы, система будет совершать колебания. Сила называется гармонической
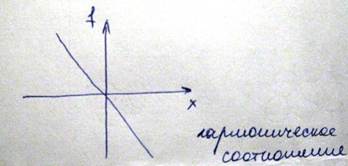
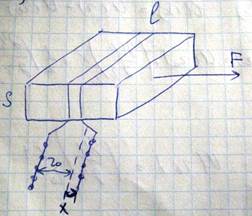
Эта растягивающая сила будет уравновешиваться внутренней силой

Модуль упругости зависит от природы атомов и от их взаимного расположения. Из опытных данных установлено, что при увеличении внешней нагрузки растут как напряжение сигма, так и относительная деформация
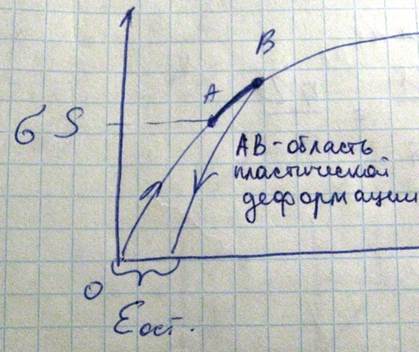
При некотором напряжении сигма с характерного для каждого материала наблюдается либо разрушение кристалла или нарушение прямой пропорциональности между сигмой и эпсилон и возникновению остаточной(пластической) деформации, не исчезающей после снятия нагрузки. В 1 случае материал является хрупким, во втором - пластичным. Напряжение сигма с при котором начинается заметное отклонение от линейности называется пределом упругости и области ОА и АВ – областями упругой и пластической деформации. В хрупких материалах предел упругости совпадает с пределом прочности и поэтому они разрушаются без видимой пластической деформации. В пластичных материалах предел упругости, как правило, значительно меньше предела прочности, поэтому разрушение пластичных материалов происходит после значительной пластической деформации. Способность кристалла к пластической деформации определяется, прежде всего, характером сил связи между его структурными элементами. Например ковалентная связь, характеризуемая строгой направленностью резко ослабляется при незначительном смещении атомов, поэтому кристаллы ковалентного типа(алмаз, кремний, германий, сурьма, висмут, мышьяк) не проявляют способности к пластической деформации, т.е. они хрупкие и разрушаются при достижении предела упругости. Металлическая связь, не имеющая направленного характера, меняется очень слабо при тангенсальном смещении атомов, поэтому кристаллы, связь которых имеют металл природу являются … Ионная связь занимает промежуточную между металлической и ковалентной, она не столь направленная, как ковалентная, и не столь гибкая, как метал.
Тепловые свойства твердых тел.
Атомы твердых тел совершают тепловые колебания относительно своих положений равновесия. Вследствие сильного взаимодействия между собой характер этих колебаний оказывается этих колебаний оказывается весьма сложным и его точное описание представляет значительные сложности. Вместо того, чтобы описывать индивидуальные колебания атомов, рассматривается их коллективное движение в кристалле как в пространственно-упорядоченной матрице. Такое упрощение основано на том, что вследствие действия значительных сил связи колебания возникшие у одной частицы немедленно передается соседним частицам и в кристалле возбуждается коллективное движение в форме упругой волны, охватывающей все частицы кристалла. Такое коллективное движение называется нормальным колебанием. Число нормальных колебаний, которое может возникнуть в решетке, равно числу степеней свободы частиц кристалла N частиц-3N колебаний. Рассмотрим одномерную модель твердого тела, как линейную цепочку атомов, способную совершать колебания в направлении перпендикулярном длине цепочки
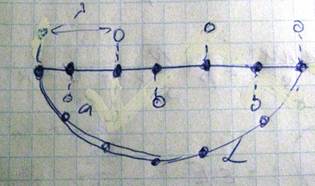
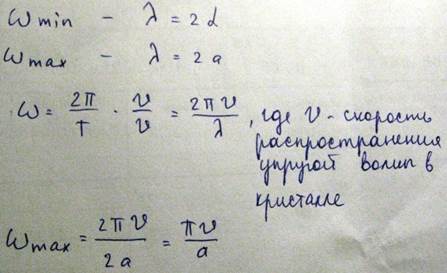
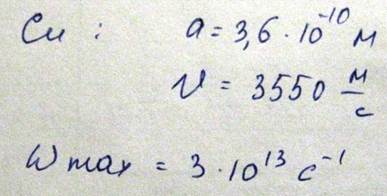
Для характеристики волновых процессов удобно пользоваться особой физической величиной, которая называется волновой вектор
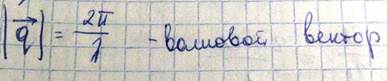
Его направление совпадает направлением распространения колебаний
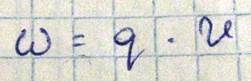
Упругие колебания кристалла называются акустическими, поскольку они включают весь спектр звуковых колебаний решетки. Упругие колебания играют основную роль в определении тепловых свойств кристалла, таких как теплоемкость, тепловое расширение, теплопроводность и некоторые другие. Одним из основных вопросов теории колебания кристаллической решетки является вопрос о распределении нормальных колебаний по частотам. сначала рассмотрим простейший случай нормальных колебаний линейной цепочки атомов

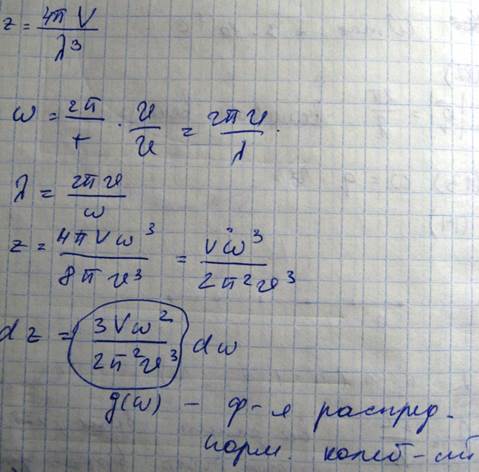
Длины волн, которые могут быть возбужденны в такой цепочки, можно найти в такой формуле
Она определяет плотность заполнения спектрального участка dw(омега) нормальными колебаниями. Так как общее число нормальных колебаний, которое может возникнуть в решетке, равно 3n, n-число частиц. Функция распределения нормальных колебаний, удовлетворяющих условию нормировки
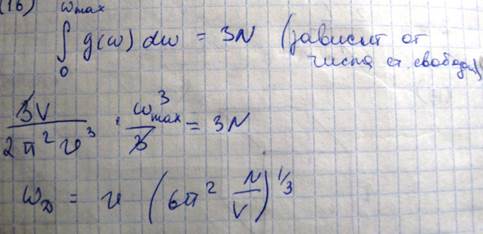
Используя известное квантово механическое соотношение

Можно получить температуру Дебая
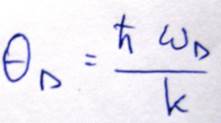
Температура Дебая это максимальная температура при нагревании выше которой в кристалле не возбуждаются дополнительные нормальные колебания. Температуры T>θD называются высокими температурами. Каждое нормальное колебание несет с собой энергию и импульс. В теории колебаний доказывается что энергия нормальных колебаний решетки равна энергии осциллятора имеющего массу равную массе колеблющихся атомов и колеблющегося с частотой равной частоте нормального колебания. И такой осциллятор называется нормальным осциллятором. Таким образом, полная энергия кристалла в котором возбужденны все 3N нормальных колебания
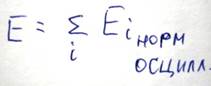
В квантовой механике энергия нормального осциллятора определяется
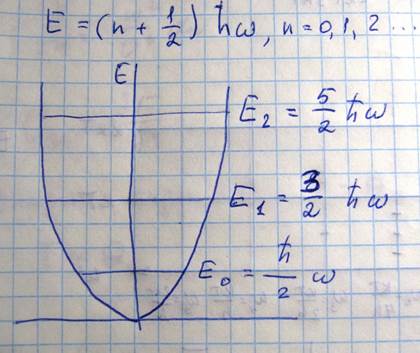
Минимальная порция энергии которую может поглотить или испустить решетка при тепловых колебаниях соответствует переходу возбуждаемого нормального колебания с данного энергетического уровня на близлежащей равна E=ћω и эта порция или квант энергии тепловых колебаний получила название Фоно. Упругие волны заполняющие кристалл можно рассматривать как газ образованный квантами нормальных колебаний решетки то есть фононами которые обладают
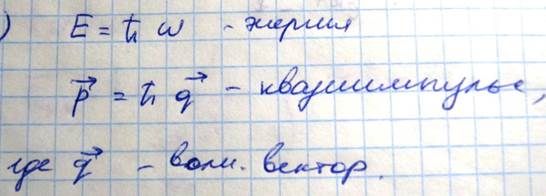
функция распределения нормальных колебаний по энергии так называемая функция Базе-Энштейна имеет след вид
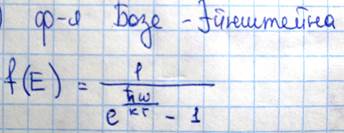
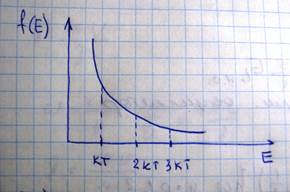
из этого графика видно что при данной температуре T в решетке возбуждаются все колебания лежащие левее температуры и практически не возбуждаются колебания с более высокими частотами. В зависимости от степени возбуждения нормальных колебаний , оно может испускать то или иное число одинаковых фононов, то есть фононов с одинаковой энергией
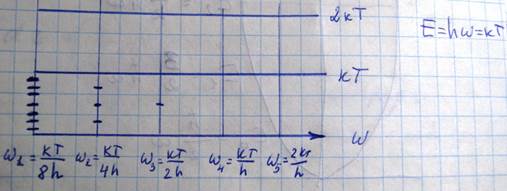
Из рисунка видно что при данной температуре колебания с частотой омега 1 возбуждено до восьмого уровня, то есть эта нормальное колебание пораждает восемь фононов. Согласно пределению функции распределения Базе-Энштейна выражает среднее число фононов имеющих данную энергию, поэтому если умножить
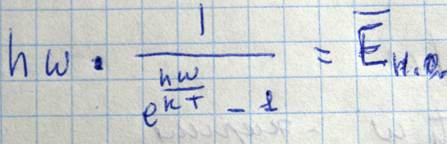
7.11.12
Дата добавления: 2015-08-08; просмотров: 1449;
