Теплоемкость

Тепловая энергия твердого тела решетки складывается из нормальных колебаний данной решетки

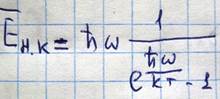
Число нормальных колебаний приходящихся на число

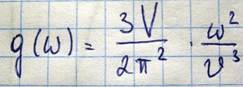
Чтобы найти полную тепловую энергию, нужно

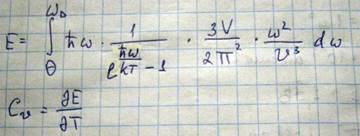
В теории тепловых свойств твердого тела очень важный вопрос: зависимость теплоемкости от температуры

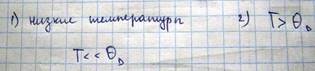
В области низких температур возбуждается главным образом низкочастотное колебание, квант энергии которых меньше, чем kT. Поэтому средняя энергия нормальных колебаний

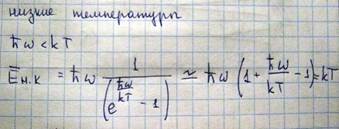
Следовательно, в области низких температур средняя энергия каждого нормального колебания изменяется пропорционально абсолютной температуре в первой степени, этот рост обусловлен тем, что с повышением температуры происходит увеличение степени возбуждения данного нормального колебания, что и обуславливает рост средней энергии. Помимо этого в области низких температур с повышением температуры происходит возбуждение нормальных колебаний (новых частот), и в число этих нормальных колебаний приблизительно

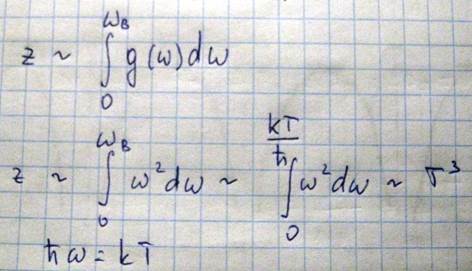
Поэтому в области низких температур, энергии кристалла, с повышением температуры, возрастает вследствие действия двух факторов: возрастание степени возбуждения каждого нормального колебания и увеличение числа нормальных колебаний

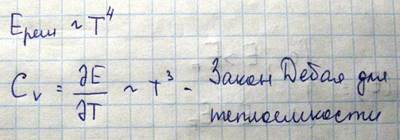
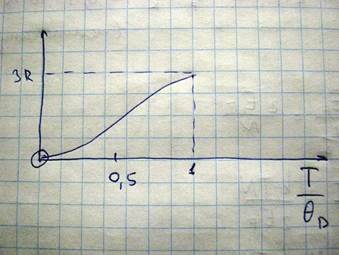
Как мы знаем при температуре, равной температуре Дебая, в твердом теле уже возбужден весь спектр нормальных колебаний, и дальнейшее увеличение температуры не приводит к появлению новых колебаний, поэтому возрастание температуры может обуславливать только увеличение степени возбуждения нормальных колебаний

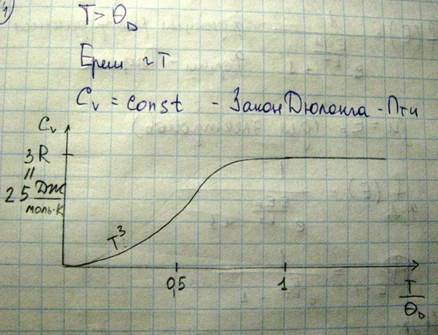
Если теперь перейдем к металлам, то в металлах помимо ионов образующих решетки и колеблющихся около своих положений равновесия, находятся также электроны, число которых в единице объема примерно такое же, как и число атомов, поэтому теплоемкость металла должна выражаться следующим образом: C_мет=С_реш + С_е.

Если бы электронный газ был обычным классическим газом, то каждый электрон обладал бы энергией 3\2kT, и

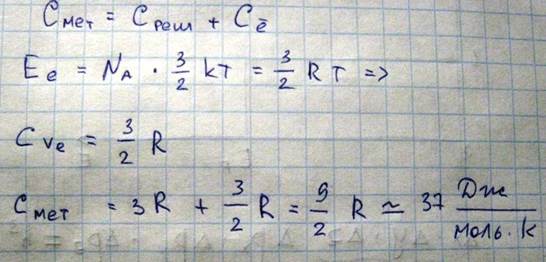
Однако эксперимент в области высоких температур показывает, что C_мет≈25Дж/моль*К. Сравнение двух цифр говорит о том, что электронный газ не вносит заметного вклада в теплоемкость металлов, это различие связано с тем что свободные электроны в металле не являются классическими частицами, а представляют собой вырожденный электронный газ свойство которого полностью объясняется только квантовой теорией.

Электроны в металле при абсолютном нуле. Энергия Ферми.

Металл для свободных электронов является своеобразной потенциальной ямой, выход из которой требует совершения работы по преодолению сил связи удерживающих электроны в металле

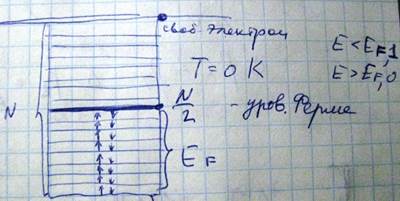
Если в металле находится n электронов, то, согласно с принципом Паули, будет занято n/2 уровней, поскольку на каждом уровне может находится только два электрона. Последний уровень, занятый электронами, называется уровень Ферми. Уровень Ферми соответствует максимальной кинетической энергии, которой может обладать электрон металле при абсолютном нуле. Таким образом, при T=0K все уровни энергии с энергией E<E_f заняты, а E>E_f свободны:

Химический потенциал - это термодинамическая функция, зависящая от макроскопических параметров, в частности от температуры, и она связана с работой которую необходимо затратить для того чтобы увеличить число частиц в системе на единицу

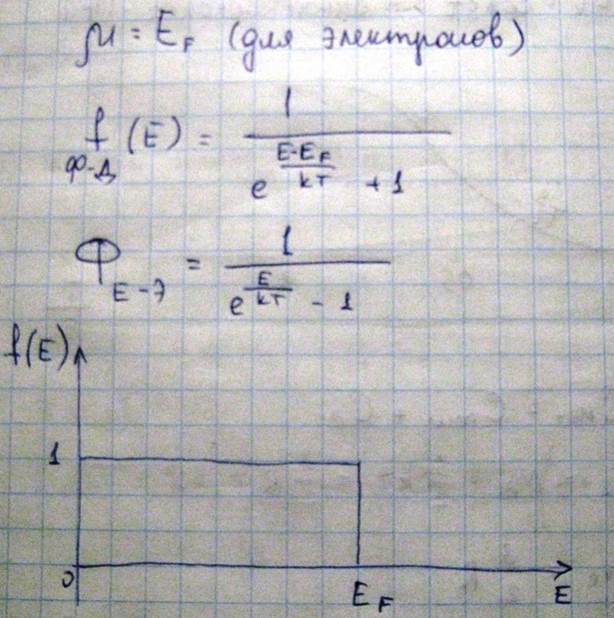
Выясним теперь, как связаны энергии Ферми с концентрацией электронов в металле. Прежде всего, получим соотношение для плотности состояния электронов в металле. Как известно, в соответствии с принципом неопределенности Гейзенберга, состояние микрочастиц, к которым относятся и электроны

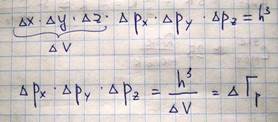
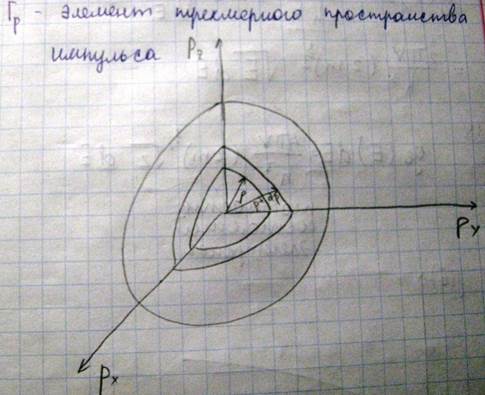
Подсчитаем число состояний, которые находятся в этом шаровом слое

Поскольку каждой ячейке отвечает одно состояние микрочастицы, то число состояний

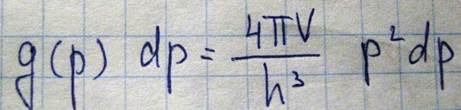
Для свободных невзаимодействующих частиц энергия импульсов связанна с таким соотношением

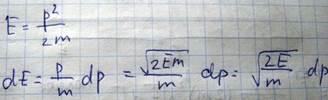
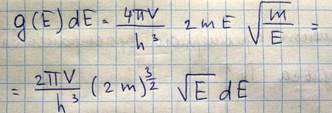
Это есть плотность состояний, выражающая число микросостояний частицы, приходящихся на единичный интервал энергии dE. В случае электронов каждой фазовой ячейке отвечает не одно, а два энергетических состояния отличающихся направлением спинов

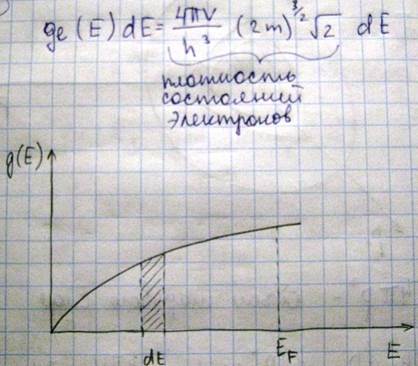
Если умножить плотность состояний электронов на функцию распределения Ферми – Дирака, то получим полную функцию распределения электронов при абсолютном нуле

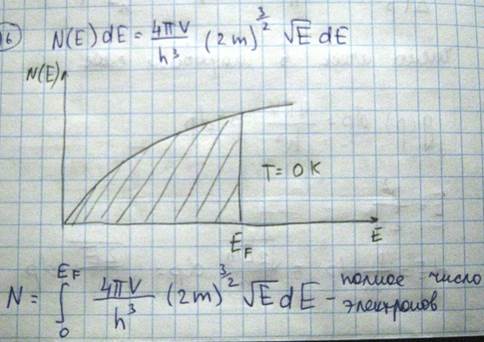
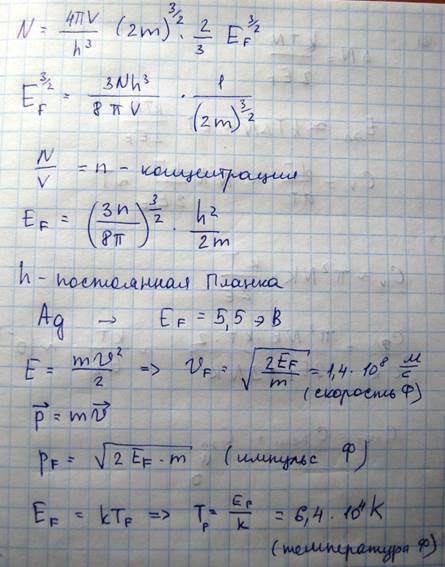
Температура Ферми показывает, при какой температуре обычный невыраженный газ (классический) с массой молекулы равной массе электрона имел бы энергию теплового движения равною энергии Ферми. Таким образом, энергия Ферми не является энергией теплового движения электронов, а имеет чисто квантовую природу, возникающую из-за специфических свойств электронов являющихся Ферми частицами подчиняющихся принципу Паули. С повышением температуры электроны подвергаются тепловому возбуждению и переходят на более высокие энергетические уровни

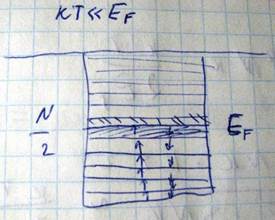
При обычных температурах, в которых энергия kT<<E_f возбуждению подвергаются электроны, лежащие в узкой полоске шириной kT. Переход электронов на более высокие уровни приводит к расплыванию функции распределения Ферми-Дирака, то есть к появлению хвоста функции распределения

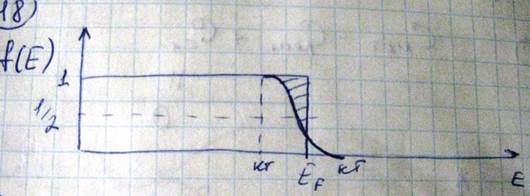
Произведем теперь приближенную оценку числа электронов переходящих на уровни выше чем уровень Ферми, если считать что эквидистантно, то ширина энергетического уровня может быть оценена

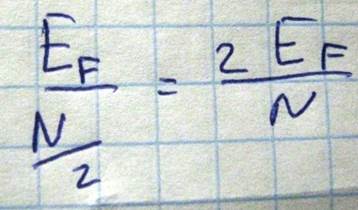
В интервале энергии kT

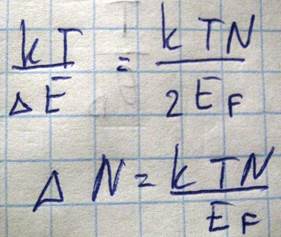
Если считать что при возбуждении на более высоколежащее, то

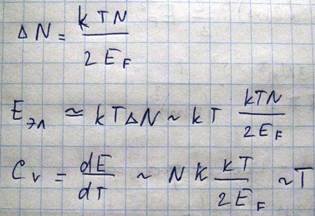
Каждый электрон подвергающийся тепловому возбуждению поглощает энергию порядка kT¸как для обычного газа. Более строгий расчет дает выражение для теплоемкости

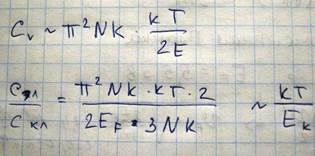
При обычных температурах теплоемкость металла определяется только теплоемкостью его решетки

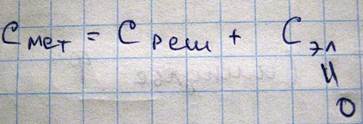
Однако иначе дело обстоит в области низких температур близких к абсолютному нулю. В это области температур теплоемкость решетки с понижением температуры в соответствии с законом Дебая убывает как T³ и вблизи абсолютного нуля может стать столь малой, что уже основное значение может принят теплоемкость электронного газа, которую как мы получили пропорционально T¹

14.11.12

Тепловое расширение твердых тел.

Для объяснения упругих свойств кристалла было введено так называемое гармоническое приближение, согласно которому силы, возникающие при смещении частиц из положения равновесия:

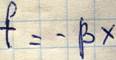
Потенциальная энергия смещенной частицы равна

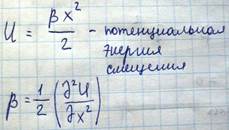
Однако с точки зрения гармонического приближения оказалось невозможным объяснение некоторых важных физических свойств, таких как тепловое расширение твердых тел и теплопроводность твердых тел.

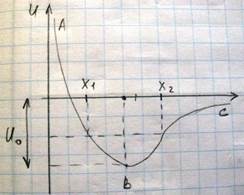
При абсолютном нуле температуры, частицы располагаются на расстоянии r₀, при этом потенциальная энергия U₀. Эти расстояния r₀ определяют размер тела при абсолютном нуле температур. С повышением температуры, частицы начинают колебаться, т.е. отклоняться от положения равновесия, и колеблющаяся частица обладает некоторой кинетической энергией. Кинетическая энергия частицы 2 достигает максимального значения в момент прохождения положения равновесия. При движении частицы 2 влево, ее кинетическая энергия затрачивается на совершение работы против сил отталкивания от частицы 1, и частица 2 останавливается там, где она обладает только потенциальной энергией. Если бы частица 2 совершала чисто гармонические колебания, то сила была бы равна

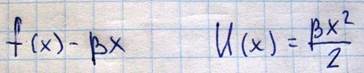
Изменение энергии описывалось бы потенциальной кривой

,

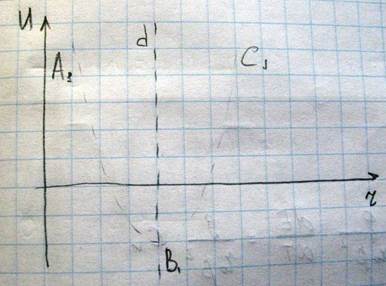поэтому смещение x₁ в левую сторону, было бы равно смещению x₂ в правую сторону, а положение равновесия не изменялось бы. Нагревание тела в этом случае сопровождалось бы увеличением амплитуды колебаний частицы 2 вправо и влево, но не происходило бы изменения положения равновесия, т.е. не происходило бы изменения размеров тела. В действительности, потенциальная кривая является не симметричной относительно Bd и ее левая часть идет круче, чем правая. А это означает, что колебания частиц в твердом теле являются ангармоническими (негармоническими), и для учета асимметрии потенциальной кривой необходимо в разложение энергии добавить слагаемое

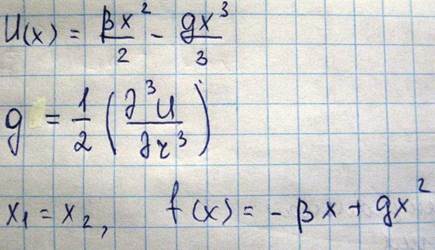
При смещении частицы 2 вправо x>0, а когда влево, то x<0. Несимметричный характер потенциальной кривой означает, что колебание частицы 2 вправо и влево являются разными, т.е. вправо частица отклоняется больше чем влево. Вследствие этого среднее положение частицы 2 также смещается вправо, а это означается увеличение расстояния между атомами, т.е. увеличение размеров тела. Произведем теперь оценку теплового расширения α, для этого найдем

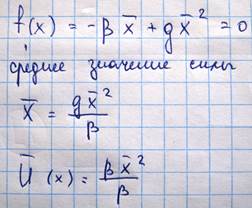
При колебаниях частицы помимо ее потенциальной энергии меняется также и кинетическая энергия, причем их средние значения равны, и полная энергия

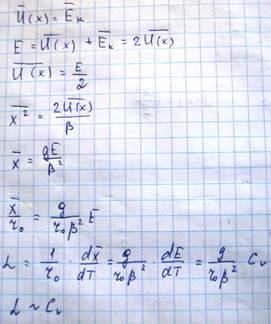
Таким образом, коэффициент линейного теплового расширения оказывается пропорциональным теплоемкости тела. Опыт подтверждает, что в области высоких температур (т.е. выше температуры Дебая) коэффициент линейного теплового расширения не …(закон Дюлонга-Пти для теплоемкости). В области низких температур коэффициент линейного теплового расширения с понижением температуры уменьшается пропорционально T³ (закон Дебая). При приближении к абсолютному нулю коэффициент линейной теплоемкости стремится к нулю. Впервые выражение для коэффициента линейной теплоемкости металлов было получено Грюнайзеном и имеет вид:

Теплопроводность

Еще одним свойством твердого тела, обусловленным ангармоническим характером колебаний атомов, является тепловое сопротивление твердого тела, обусловленное его теплопроводностью. Тепловое сопротивление не могло бы возникнуть, если бы атомы совершали строго гармонические колебания, распространяющиеся в решетке в виде невзаимодействующих упругих волн. Отсутствие взаимодействия между волнами позволяло бы им распространяться им в кристалле подобно световой волне в вакууме. Если бы в таком кристалле можно было бы создать разность температур, то атомы в горячей области кристалла, колеблющиеся с большими амплитудами, передавали бы свою энергию соседним атомам, и фронт тепловой волны распространялся бы вдоль кристалла со скоростью звука. Так как эта волна не встречала бы никакого сопротивления, то даже при бесконечно малой разности температур, тепловой поток мог бы достигать сколь угодно больших значений, и теплопроводность такого кристалла была бы бесконечно большой. В реальных кристаллах при не слишком низких температурах колебания атомов носят ангармонический характер. Появление ангармоничности приводит к тому, что нормальные колебания теряют независимый характер и при встречах взаимодействуют друг с другом, обмениваясь энергией и меняя направление своего распространения, т.е. рассеиваясь друг на друге. Переход к ангармоничности эквивалентен введению взаимодействия между фононами, которые называются фонон-фононное взаимодействие. Рассеивание фононов затрудняет процесс передачи энергии путем теплопроводности. Вероятность протекания фонон-фононового рассеяния, как и вероятность протекания других процессов рассеяния характеризуется обычно эффективным сечением рассеяния. Если по отношению к процессам рассеяния принять что фонон является шариком

Поскольку рассеяние появляется в результате ангармонического характера колебаний атомов, количественной мерой которого является константа ангармонизма g, то естественно считать, что

Зная эффективное сечение можно вычислить среднюю длину свободного пробега фонона, которая пропорциональна

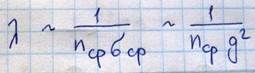
В кинетической теории газов получили выражение для теплоемкости

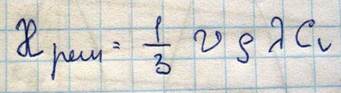
Эту формулу можем применить к фононному газу

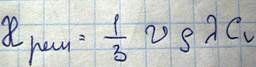
v-скорость звука в кристалле. В области высоких температур:

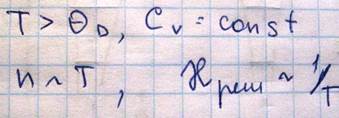
В области низких температур концентрация фононов резко уменьшается при понижении температуры, что приводит к возрастанию длины свободного пробега λ_ср, которая в переделе стремится к размерам кристалла и уже не зависит от температуры, поэтому в области низких температур теплопроводность решетки пропорциональна теплоемкости решетки, т.е. Т³- закон Дебая

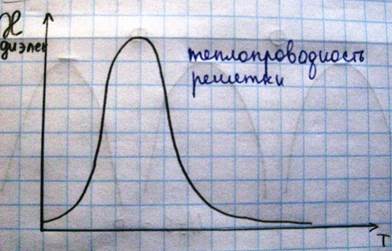
Если рассмотрим металлы, которые, как известно, помимо решетки состоят также из электронов, то

.

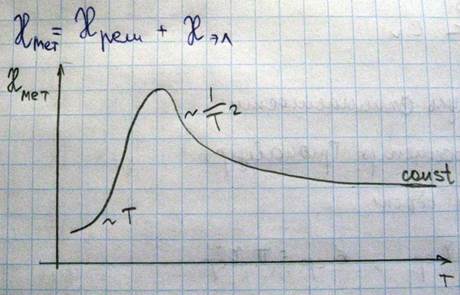Зонная структура твердых тел

В твердом теле расстояние между атомами настолько малы (10^-10), что каждый из атомов оказывается в достаточно сильном поле соседних атомов. Для того, чтобы проследить, какое влияние оказывает это поле на энергетические уровни рассмотрим идеализированный пример

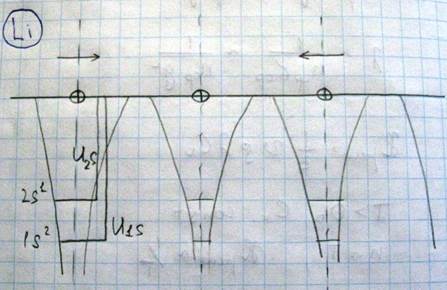
Поскольку атомы, находясь на таком расстоянии, не взаимодействуют друг с другом, энергия состояния в атоме будет такой же, как в отдельном изолированном атоме. Видно, что изолированные атомы отделены друг от друга потенциальными барьерами и шириной. Высота барьеров для электронов, находящихся на различных энергетических уровнях, будет различна. Начнем сближать атомы, сохраняя ту же самую структуру

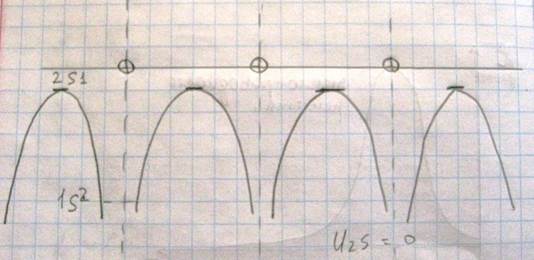
Из этого рисунка видно, что резко изменилась высота потенциального барьера. Такие обобществленные электроны - их совокупность называется электронным газом. Вследствие резкого уменьшения глубины и ширины потенциального барьера свободу перемещения по кристаллу получают не только валентные электроны, но и электроны, расположенные на других уровнях атома, причем перемещение этих электронов происходит туннельным образом. Движение электронов в кристалле можно описать

Если обобществленные электроны сохраняют достаточно сильную связь со своими атомами (приближение сильной связи), то их потенциальную энергию рассматривают так. Различие между кристаллом и отдельным атомом заключается в следующем: если в изолированном атоме данный энергетический уровень Ea характеризуемый квантовыми числами n-главное квант числоl-орбитальное квантовое число, определяющее энергию электрона в атоме, является единственным в атоме, то в кристалле, который содержит N атомов этот уровень повторяется N раз. Иначе говоря, каждый уровень изолированного атома оказывает N-кратно вырожденным в кристалле. Такое вырождение называется перестановочным вырождением. Таким образом, уровень s в кристалле дает зону S, состоящую из N подуровней, и в которой находится 2N электронов. Расстояние между энергетическими подуровнями в зоне кристалла очень мало

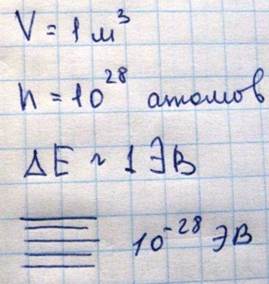
Эта величина столь мала, что зону можно считать непрерывной, однако тот факт, что число уровней все-таки конечно играет важную роль в определении характера распределения электронов по энергетическим расстояниям. Наибольшее влияние внутрикристаллическое электрическое поле решетки на внешние валентные электроны атомов, поэтому состояния этих электронов в кристалле претерпевают наибольшие изменения. И энергетические зоны, образованные этими электронами оказываются наиболее широкими, внутренние же электроны, наиболее сильно связанные с ядром, испытывают лишь незначительное возмущение от соседних атомов, так что их энергетические уровни в кристалле оказываются такими же узкими

21.11.12

Выясним теперь, как зависит энергия электронов от их импульса E=E(p). Как мы с вами помним, для описания состояния электронов нужно решить уравнение Шредингера

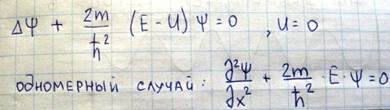
Решение этого дифференциального уравнения можно искать в таком виде

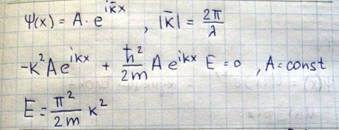
Закон дисперсии:

Как известно квадрат модуля волновой функции пропорционален вероятности обнаружения электрона в той или иной области пространства. В случае свободного электрона:

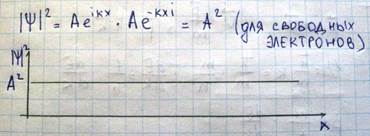
Свободный электрон может быть обнаружен в любой точке пространства. Вероятность нахождения в любой точке пространства одинакова. Иначе дело обстоит в случае электрона движущегося в периодическом поле кристалла образованном правильно(регулярно) расположенными ионами решетки

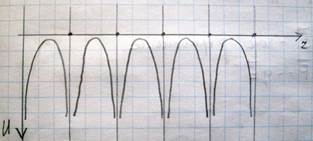
В этом случае вероятность обнаружения электрона в данном месте кристалла должна быть периодической функцией координаты, так как положение отличающееся друг от друга на величину равную периоду решетки??? Различным только может быть положение электронов в пределах одного периода.

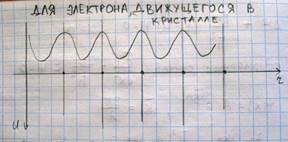
А это означает что амплитуда волновой функции в случае электрона движущегося в кристалле

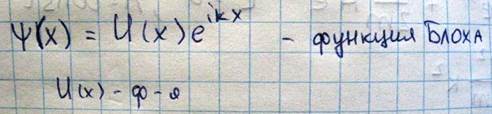
Эта амплитуда должна быть периодической функцией. Рассмотрим теперь движение электронов в кристалле из связей между импульсом и скоростью

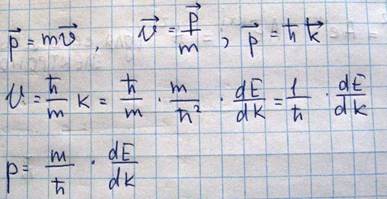
Оказываются справедливыми эти выражения для скорости и импульса электрона не только в случае свободных электронов, но и так же для электронов движущихся в периодическом поле решетки. Импульс в этом случае называется квази-импульсом электрона. Зададим в кристалле электрическое поле 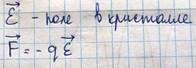, сообщая электрону ускорение

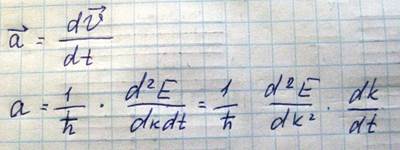
Эта сила F действую на электронов в течение времени dt совершит элементарную работу

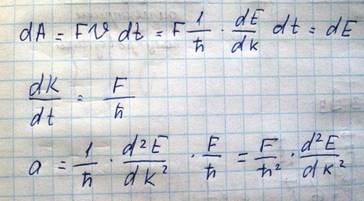
Данная формула для ускорения устанавливает взаимосвязь между ускорением электрона и внешней силой действующей на этот электрон. В случае движения электрона в кристалле роль массы играет величина -эффективная масса электрона. Приписывая электрону находящемуся в периодическом поле кристалла, массу m* можно уже считать электрон свободным и описывать его движение во внешнем поле так, как описывается движение в случае свободного электрона. Из этой формулы видно что эффективная масса зависит от знака производной энергии по k- волновому вектору. И она может быть как положительной так и отрицательной

Изменяющиеся значений эффективной массы электрона в кристалле обусловлена тем, что в кристалле полная энергия электрона E_{эл.крист}=U+E_k, E_{эл.своб}=E_k. При движении электрона под действием внешней силы, часть работы этой силы может перейти в кинетическую энергию, а часть в потенциальную. В случае свободного электрона вся работа внешней силы переходит в кинетическую энергию, следовательно, доля работы переходящая в кинетическую энергию в кристалле будет меньше, что означает уменьшение скорости движения электрона, а это соответствует возрастанию массы. В предельном случае, когда вся работа внешней силы переходит в потенциальную энергию электрона, он будет вести себя в кристалле как частица с бесконечно большой массой. Если же при движении электронов в кристалле потенциальную энергию будет переходить не только вся работа внешней силы, но и часть кинетической энергии электрона, то по мере движения такого электрона его скорость будет уменьшаться. он будет замедляться, то есть он будет вести себя как частица с отрицательной массой. В кристалле масса электрона переменная величина. Каждая энергетическая зона содержит ограниченное число энергетических уровней (равное число атомов), и в соответствии с принципом Паули на каждом уровне моет находиться не более двух электронов. При ограниченном числе электронов содержащихся в кристалле заполненными окажутся лишь наиболее низкие энергетические уровни. По характеру заполнения зон электронами все вещества в природе можно разделить на две большие группы. К первой группе относятся вещества у которых над полностью заполненной зоной располагаются зоны, заполненные лишь частично, такие зоны возникают в том случае когда атомный уровни с которых она образована, заполнена лишь частично. Такая ситуация например реализуется в случае щелочных элементов. Наличие зоны заполненной лишь частично присуще металлам. Ко второй группе веществ относятся вещества, у которых над полностью заполненной зоной располагается пустая зона. Типичным и примерами являются химические элементы 4 группы таблицы Менделеева, такие как углерод в модификации алмаза, кремний, германий, серое олово, так же имеющее модификацию алмаза. К этой же группе веществ относятся и многие химические соединения. В том числе окислы металлов (нитриты. карбиты и т.д.)

Рассмотрим теперь поведение во внешнем электрическом поле электронов находящихся в частично заполненных и полностью заполненных зонах . Эта сила будет стремиться нарушить симметрию в распределении электронов по скоростям, она будет ускорять электроны, движущиеся по направлению силы и замедлять электроны, движущиеся в противоположном направлении, так как подобные воздействия связано с изменением энергии, то оно означает переход электрона в новое квантовое состояние с большей или меньшей энергией. Такие переходы возможны лишь в том случае, когда в зоне, к которой относиться данный электрон имеется не занятое состояние. В этом случае в кристалле возникает преимущественной движение электронов обуславливающие возникновение электрического тока, и такие вещества являются хорошими проводниками. Пусть теперь валентная зона заполнена полностью, и она отделена от близлежащей свободной зоны широкой энергетической щелью, внешнее электрическое поле, не способно сообщить электронам энергию достаточную для перехода в свободную зону. Поэтому под действием поля может происходить лишь перестановки электронов внутри заполненной зоны, что не нарушает распределение электронов по скоростям, следовательно, в таких веществах приложение электрического поля не может вызвать направленного движения электронов, то есть они обладают нулевой электропроводностью. По ширине запрещенной зоны вещества второй группы делятся на две подгруппы:

1) если Eg>3Эв - относятся к классу диэлектриков;

2) если Eg<1Эв, то эти вещества называются полупроводники.

Рассмотрим теперь, как происходит движение электронов в проводниках

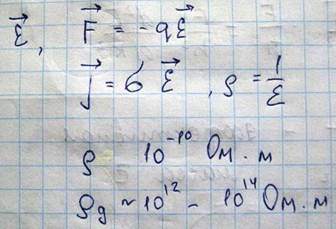
Возникновение тока в проводнике свидетельствует о том, что под действием поля электроны приобретают направленное движение, и функция распределения электронов по состоянию изменяется. Такое направленное движение электронов называется дрейфом, и средняя скорость такого движения называется скорость дрейфа

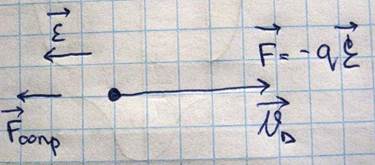
Под действием силы F электрон должен двигаться ускоренно и его скорость должна непрерывно возрастать, однако при своем движении электрон сталкивается с дефектами решетки и рассеиваясь на них теряет скорость действие решетки можно формально учесть введя силу сопротивления, зависящую от скорости движения электрона

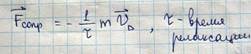
При этом уравнение динамики электрона может быть записано в виде:

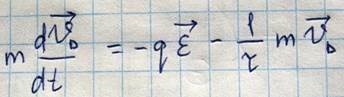
Из этого уравнения видно, что после включения поля E скорость электрона будет возрастать до тех пор, пока сила сопротивления не уравновесит силу, действующую со стороны действующего поля, после этого скорость будет равномерна

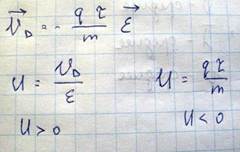
Зная скорость дрейфа электронов легко вычислить плотность электрического тока и удельную электропроводность проводника

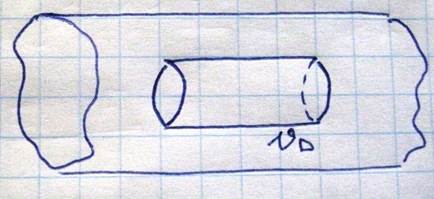
С этой целью в объеме проводника выделим цилиндр с площадью основания 1 и длинной равной скорости дрейфа, за одну секунду через его основание пройдут все электроны, находящиеся в объеме этого цилиндра

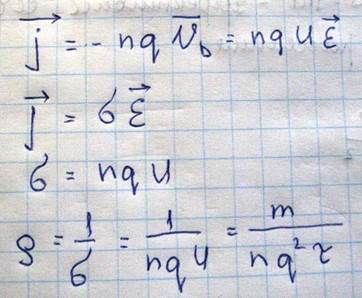
Движение электронов кристалле удобно описывать, вводя понятие длина свободного пробега в кристалле. По аналогии с движением молекул в кинетической теории газа можно считать, что электрон в кристалле движется прямолинейно до тех пор пока он не испытает соударения с дефектом решетки. Дефектом решетки на которых происходит рассеяние электронов сопровождающееся обменом энергии и импульса, прежде всего является тепловые колебания решетки то есть фононы, а так же примесные атомы. Средний отрезок пути, который проходит электрон между двумя последовательными соударениями, называется длина свободного пробега и обозначается λ. Если бы электрон уже в единичном акте рассеяния полностью терял скорость в данном направлении движения и возвращался в первоначальное состояние хаотического движения, то средняя длина свободного пробега была бы равна λ=υτ. Часто, однако для полного уничтожения скорости в заданном направлении требуется не одно, а в среднем ν соударений с рассеивающими центрами, и теперь уже средний путь, который походит электрон, будет равен не λ, а будет 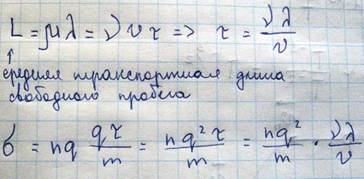– средняя транспортная длина свободного пробега. В случае невырожденного электронного газа, при котором плотность заполнения зон проводимости настолько мала, что они практически никогда не встречаются так близко, чтобы их состояние могло определяться принципом Паули. Поэтому эти электроны могут считаться свободными в том смысле, что на движение любого электрона другие электроны не оказывают никакого влияния. В этом случае выражение для электропроводности определяется через среднее значение числа соударений

В случае вырожденного электронного газа, поведение которого описывается статистикой ферми Дирака внешнее поле может влиять только на электроны расположенные вблизи уровня ферми и величина электропроводности описывается так

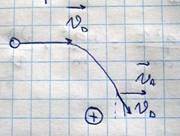
Рассмотрим теперь вопрос о зависимости подвижности носителей заряда от температуры. 1 область высоких температур 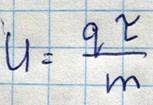. В области высоких температур основное значение имеет рассеяние электронов на тепловых колебаниях решетки (на фонон) каждый атом решетки совершает беспорядочное колебание около положения равновесия оставаясь в пределах сферы радиуса а равной амплитуде колебаний

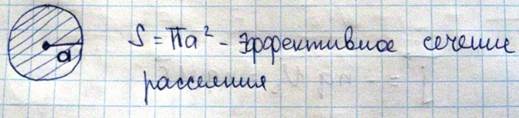
Каждый электрон, проходя по проводнику, попадая в один из таких дисков, будет испытывать рассеяние и при прочих равных условиях, вероятность попадания электронов в такой диск λ~1/S~1/a². Как известно, энергия колеблющегося атома пропорциональна E~a²~T, поэтому в области высоких температур длина свободного пробега электрона обусловлена рассеянием на фононах λ~1/T. Если принять что число столкновений равным 1, то σ~T^-1/T^1/2=T^3/2- для невырожденного газа. Для вырожденного σ~T^-1/const=T^-1. В области низких температур основное значение имеет рассеяние на ионизованных примесных атомов, и рассеяние состоит в том что ионы примеси отклоняют электроны пролетающие мимо них и тем самым, уменьшают скорость электронов в заданном направлении

28.11.12

Сверхпроводимость

В 1911 г голландский физик Камерлинг - Оннес изучая сопротивление ртути при низких температурах обнаружил, что при Tс=4.15K ее сопротивление резко уменьшается до нуля

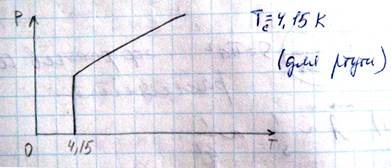
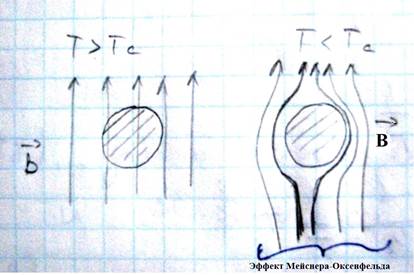
– это явление было названо сверхпроводимостью. Затем это явление было открыто для многих других металлов и сплавов. Температура, при которой сопротивление обращается в ноль, получила название критической температурой. Для сверхпроводящего состояния характерно также, что магнитное поле не проникает в объем сверхпроводника, то есть сверхпроводящие материалы являются идеальными диамагнетиками

.

Этот эффект называется эффект Мейснера-Оксенфельда. Достаточно сильное внешнее магнитное поле разрушает сверхпроводящее состояние и значение магнитной индукции, при котором это происходит, называется критическим полем и обозначается B_k. B_k=B_k(T) - является функцией температуры. Фазовая диаграмма сверхпроводника:

Если увеличивать силу тока, протекающего по сверхпроводнику, то при некотором значении силы тока сверхпроводящее состояние разрушается, когда магнитное поле создаваемое этим током на поверхности сверхпроводника превышает значение критического поля. Этот ток называется критическим током и зависит от температуры. По характеру проникновения магнитного поля в сверхпроводник все сверхпроводящие материалы разделяются на две большие группы, а именно сверхпроводники первого и второго рода.

В сверхпроводниках первого рода проникновение магнитного потока в них не происходит до тех пор, пока внешнее магнитное поле не превысит значение критического магнитного поля.

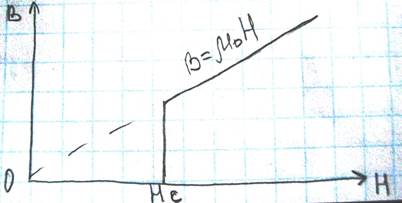
В сверхпроводниках второго рода существует два значения критического поля H_c1 и H_c2.

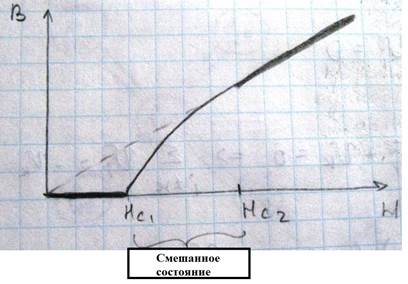
При H_c1<H<H_c2 возникает смешанное состояние, которое представляет собой совокупность сверхпроводящих областей и областей нормальной фазы, причем сверхпроводящие области состоят из так называемых вихрей Абрикосова. Долгое время сверхпроводящее состояние различных металлов и соединений удавалось получить лишь при очень низких температурах достижимых с помощью жидкого гелия. К началу 1986 года максимальная температура сверхпроводящего перехода 23.7К (Nb₃Sn). А в 1986 году Беднорц и Мюллер, открыли материалы, у которых сверхпроводящий переход имеет очень высокую температуру, а именно купратные сверхпроводники La₂CuO_4-δ, у которого T_c≈40K и YBa2Cu3O_7-δ, у которого T_c≈90K (высокотемпературная сверхпроводимость). В них была реализована температура 90К, к настоящему моменту рекорд таких соединений Тс~127К. Огромный интерес к явлению высокотемпературной сверхпроводимостью (ВТСП (HTSC)) обусловлен в частности тем, что если удастся создать материалы с критической температурой порядка 300К, то произойдет настоящая техническая революция. Например, использования создания сверхпроводящих электропроводников, позволят свести к нулю потери на тепло. В настоящий момент класс высокотемпературных сверхпроводящих материалов непрерывно расширяется. К настоящему моменту разработана теория сверхпроводимости классических сверхпроводящих материалов так называемой теорией БКШ (Бардин, Купер, Шриффер). Теория сверхпроводимости является очень сложной квантовой теорией, далеко уходящей за рамки нашего курса, и в основе теории лежит образования так называемых куперовских пар, в которые могут объединяться два электрона, преодолевая кулоновское отталкивание, имеют заряд -2e и равные, но противоположно направленные спины. Особенностью куперовских пар является то, что они могут перемещаться под действием электрического поля не рассеиваясь на решетке, то есть для них сопротивление является нулевым. В куперовские пары объединяются электроны занимающие состояние в узкой энергетической полосе вблизи уровня Ферми. К настоящему моменту теория высокотемпературной сверхпроводимости пока не создана.

Полупроводники

Химически чистые полупроводники называются собственными полупроводниками. К ним относятся ряд чистых элементов таких как Ge, Si, Se, Te, а так же многие химичекие соединения такие как GaAs, InSe, GaSe и т.д. Упрощенная схема зонной структуры собственного полупроводника при Т=0К представляет следующий вид:

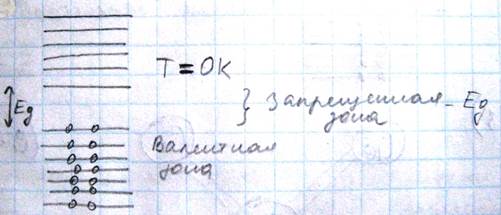
Поэтому при абсолютном нуле собственный полупроводник, как и диэлектрик, обладает нулевой проводимостью. Однако с повышением температуры в следствие термического возбуждения электронов валентной зоны, часть из них получает возможность перейти в валентную зону оставляя при этом незанятое состояние в валентной зоне. И ри приложении к такому проводнику электрического поля в нем возникает направленное движение электронов зону проводимости и валентной зоны приводящие к возникновению электрического тока, и кристалл становится проводящим. Чем уже ширина запрещенной зоны и чем выше температура, тем больше электронов будет переходить в зону проводимости и тем большую проводимость будет приобретать этот полупроводник. Отсюда вытекает два важных вывода:

1) проводимость полупроводников является возбужденной, она появляется под действием внешних факторов, способных сообщить электронам достаточную энергию для перехода электронов из валентной зоны в зону проводимости. Такими факторами могут быть нагревание, облучение электромагнитными волнами (в частности светом), бомбардировкой ионизирующим излучением;

2) разделение веществ на полупроводники и диэлектрики носит в значительной степени условный характер. Например, алмаз, являющийся при комнатной температуре хорошим диэлектриком, при нагревании становится полупроводником.

Рассмотрим теперь более подробно поведение электронов в валентной зоне, в которой возникли свободные, то есть не занятые энергетические состояния вследствие перехода электронов в зону проводимости. В том случае, когда валентная зона заполнена полностью

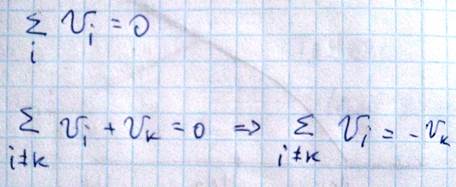
Если в валентной зоне отсутствует k-тый электрон то сумма скоростей всех остальных электронов будет равняться –vk и заряд который при этом может быть перенесен

(-e)(-V_k)=eV_k

Полупроводники любой степени чистоты всегда содержат примесные атомы создающие свои собственные энергетические уровни, получившие называние примесные уровни. Эти уровни могут располагаться как в запрещенной, так и в валентной зоне проводника

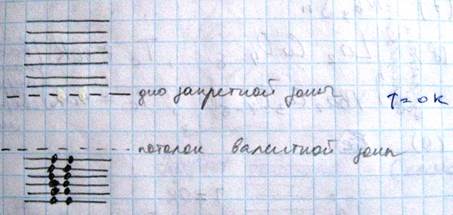
на различных расстояниях как в разрешенных зонах, так и в запрещенных, вблизи дна или потолка, и существенно влиять на свойства полупроводников. Рассмотрим основные типы примесных уровней. Пусть в кристалл четырех валентного Ge будет добавлено в небольшом количестве примесные атомы As имеющего валентность +5

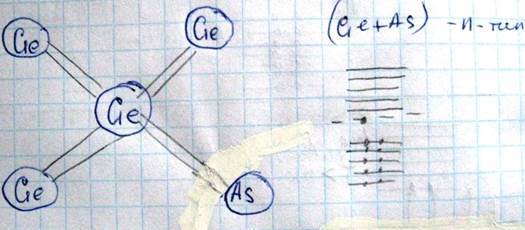
Если вместо одного атома Германия сядет атом Мышьяка, то 4 валентных электрона этого атома пойдут на образование связи с 4 соседними. а оставшийся пятый электрон мышьяка образует примесный уровень, располагающийся в запрещенной зоне германия вблизи дна зоны проводимости. При T>0 эти электроны могут переходить в зону проводимости и участвовать в проводимости. Примеси, являющиеся источником электронов в зоне проводимости, называются донорами.(As- донор). Энергетические уровни примесей называются донорными уровнями. Сам полупроводник называется донорным проводником или проводником n-типа или электронный проводник.

(Ge+In)- p-тип:

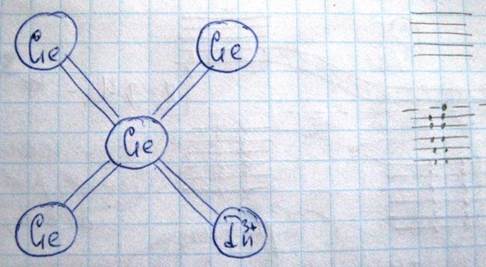
Этому атому индия для образования ковалентной связи со своими соседями к этим трем электронов не хватает четвертого. И вот атом индия занимает недостающий электрон из валентной зоны германия, образуя таким образом примесный уровень вблизи потолка валентной зоны. При этом в валентной зоне германия образуется дырка. Примесь, которая захватывает электроны из валентной зоны, называется акцепторной примесью. Уровень - акцепторный уровень. Полупроводник с акцепторной примесью - дырочный полупроводник, или акцепторный полупроводник, или полупроводник p-типа. При температурах, отличных от абсолютного нуля, в полупроводнике происходит процесс возбуждения или, как иногда говорят, генерации свободных носителей заряда. Если бы этот процесс был единственным в кристалле, то концентрация носителей непрерывно возрастала бы с течением времени. Однако, наряду с процессами генерации носителей в полупроводниках, протекает процесс их рекомбинации. Он состоит в том, что свободный электрон ( то есть электрон в зоне проводимости) при встрече с вакантным местом (то есть дыркой) занимает это место, в результате чего происходит уничтожение пары свободных носителей, то есть электрон и дырка теряют свою подвижность

При любой температуре между процессом тепловой генерации носителей и процессом их рекомбинации устанавливается равновесием, которому соответствует равновесная концентрация носителей и такие носители называются равновесные. Помимо теплового возбуждения возможны и другие способы генерации свободных носителей в полупроводниках, как то облучением света, облучением ионизирующим излучением, инжекцией (впрыскиванием) через контакт за счет электрического поля. В результате чего появляются дополнительные избыточные против равновесных концентрации свободных носителей, и эти носители называются неравновесные носители. Процесс перехода электрона из зоны проводимости в валентную зону при рекомбинации может осуществляться двумя способами:

1) переход через запрещенную зону:

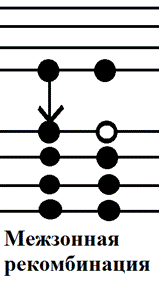
2) переход сначала на примесный уровень, а с него в валентную зону:

При обоих типах переходов освобождается каждый раз одна и та же энергия равная ширине запрещенной зоне. Выделение энергии может происходить или в виде излучения квантов света или в виде выделения тепла- возбуждение фононов. Первый тип рекомбинации называется излучательная рекомбинация. Второй – безизлучательный. В частности процесс излучательной рекомбинации лежит в основе действия источников когерентных (лазеров на полупроводниках) излучения (GaAs-лазерная указка).

Контактное явление в полупроводниках (pn- переход)

Электронно-дырочный переход образуется на границе между полупроводниками p-типа и n-типа. P-n является основным переходом для полупроводников. P-n переход представляет собой некоторую область внутри кристалла на границе между его частями с разным типов проводимости p-тип – Ge+In, n-тип – Ge+As . Будем считать, что создание идеального электрического контакта между кристаллами n и p типа возможно путем их простого соприкосновения, если между кристаллами нет контакта и электроны не могут переходить из одного кристалла в другой, то уровни Ферми располагаются в них на разной высоте, а именно (20). Оба кристалла являются электрически нейтральными, то есть в любом участке своего объема заряды ионизованных атомов полностью нейтрализованы зарядами противоположного знака свободных носителей. В кристалле p-типа основными носителями заряда являются дырки, которые в основном образуются благодаря наличию в кристалле акцепторной примеси. А в кристалле n-типа основным носителем заряда являются электрона, образующиеся за счет донорной примеси и неосновными носителями заряда являются дырки, которые образуются за счет собственных атомов кристалла. Если теперь между обоими кристаллами создать электрический контакт, в результате чего свободные носители заряда получат возможность переходит из одного кристалла в другой, то кристаллы образуют единую систему и уровни Ферми у этих кристаллов установятся на одинаковой высоте(21),где U_k-контактная разность потенциалов. В результате чего тут возникнет потенциальный барьер, высота которого будет равна φ. При создании контакта между кристаллами через этот контакт из одного кристалла в другой устремляются диффузионные потоки свободных носителей, то есть электронов и дырок. В кристалле p типа основными носителями заряда являются дырки, они в первую очередь будут переходить во второй кристалл, по этой же причине из кристалла n типа в кристалл n типа будут переходить электроны. Электроны переходя из кристалла n-типа в p-тип будут рекомбинировать с дырками, причем рекомбинация происходит в тонком слое этого кристалла, примыкающем к границами кристалла. В результате отрицательный заряд акцепторной примеси в это случае уже не компенсируется положительным зарядом дырок, и этот слой заряжается отрицательно. Контактное электрическое поле которое направленно от кристалла n-типа к кристаллу p-типа.

05.12. 12

Диффузионный ток - движение основных носителей

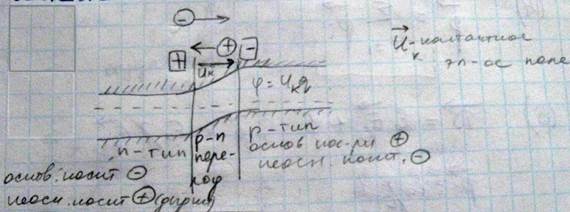
Через область pn перехода помимо диффузионного тока возникает движение неосновных носителей (дрейфовый ток). В отсутствие внешнего электрического поля, величина диффузионного тока равна величине дрейфового тока, и поэтом результирующий ток через контакт равен нулю. Приложим внешнее электрическое поле, и будем считать, что внешние напряжение положительно, если потенциал кристалла p типа больше (положительнее) чем потенциал кристалла n типа. В этом случае внешнее электрическое поле будет направлено от кристалла p типа к кристаллу n типа, то есть оно будет направленно против контактного поля, при этом будет понижаться величина потенциального барьера

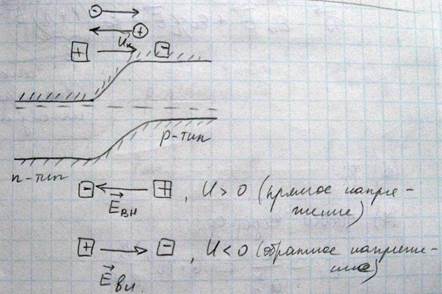
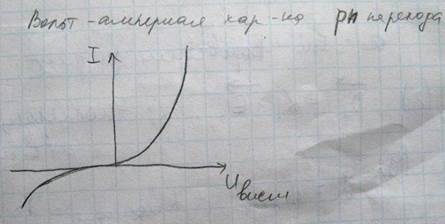
Будем считать внешнее напряжение отрицательным, если потенциал кристалла n типа будет больше, то есть положительнее, чем потенциал кристалла p типа. И в этом случае внешнее поле будет складываться контактным полем, то есть величина барьера возрастет. Изменение величины потенциального барьера приведет к изменению величины диффузионного тока, то есть тока основных носителей. Изменение величины потенциального барьера не оказывает заметного воздействия на величину дрейфового тока. И в результате этого полный ток, текущий через контакт, уже не будет равен нулю. Вольтамперная характеристика pn перехода не линейная.

Диэлектрики.

При помещении в электрическое поле диэлектриков, они не проводят электрический ток. Однако в их атомно-электронной структуре и электрическом состоянии это поле вызывает ряд изменений называемых электрической поляризацией. Вектор электрической поляризации

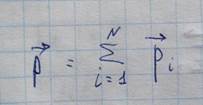
Диэлектрические свойства вещества характеризуются диэлектрической проницаемостью, восприимчивостью, индукцией, поляризацией

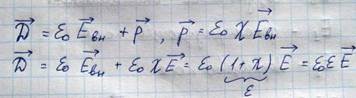
Для того чтобы лучше представить картину поляризации кристалла диэлектрика в электрическом поле, рассмотрим сначала поляризуемость одиночного атома. В свободном атоме центр тяжести электронного облака усредненного по времени совпадает с ядром и электрический момент атома равен нулю. Внешнее электрическое поле вызывает деформацию электронного облака (смещения) относительно ядра, и индуцирует в нем электрический момент. Величина момента зависит от напряженности поля и деформируемости электронной оболочки, определяемой соотношением напряженности внешнего поля и внутреннего атомарного поля

Эта величина значительно больше технически достижимых полей, следовательно, внешнее поле можно считать слабым по отношению к внутреннему, и считать что электрический момент атома, с достаточной точностью просто пропорционален напряженности внешнего поля

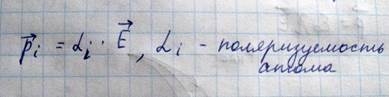
Вне полярных молекулах и кристаллах механизм поляризуемости аналогичен электронному механизму поляризуемости атома, и в первом приближении поляризуемость вещества равна сумме поляризуемостей отдельных атомов, для неполярных молекул. В полярных молекулах содержатся ионы с несовпадающими центрами тяжести положительных и отрицательных зарядов, следовательно, они обладают собственным дипольным моментом и собственный дипольный момент молекулы в этом случае равен векторной сумме составляющих дипольных моментов. Если такое вещество поместить в электрическое поле, то возможны три основных механизма поляризации: 1) электронная поляризуемость атомов и ионов, составляющих молекулы или кристалл; 2) ионная поляризуемость связанная с удалением друг от друга противоположно заряженных ионов; 3) ориентационная поляризуемость связанная с поворотом молекул в электрическом поле. В общем виде для веществ с полярными молекулами

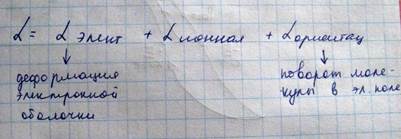
В этом выражении последнее слагаемое сильно возрастает с понижением температуры, поскольку тепловое движение молекул, которое пропорционально температуре, нарушает упорядоченное расположение молекул. Расчет действующего на атом или ион электрического поля обусловленного поляризацией образца в целом является одной из важнейших задач в теории диэлектриков. Предположим, что образец имеет форм эллипсоида вращения, одна из осей которого направлена параллельно направлению внешнего электрического поля. В этом случае так называемое локальное поле может быть вычислено по следующей формуле

Поле, создаваемое в месте нахождения атома или иона зарядами, находящимися на поверхности воображаемой полости E2. В случае Е3=0 – случай в изотропных телах и кубических решетках. Изменить состояние поляризации диэлектрика можно не только за счет внешнего электрического поля, но также и за счет внешних механических деформаций изменяющих величину и направление элементарных диполей, такие вещества называются пьезоэлектриками. Вещества, у которых даже в отсутствие внешнего электрического поля существует самопроизвольный(спонтанный) электрический дипольный момент, то есть центр тяжести отрицательного заряда не совпадает с центром тяжести положительного заряда, называются сегнетоэлектриками. В таких кристаллах соседние диполи стремятся ориентироваться параллельно друг другу вследствие взаимодействия между собой, причем это стремление передается в кристалле от атома к атому, так что целый макроскопический области называемые доменами обладают суммарной спонтанной поляризацией в заданном направлении. Поляризация p в сегнетоэлектриках зависит от внешнего электрического поля нелинейно и следовательно диэлектрическую восприимчивость таких материалов определить достаточно сложно. Наиболее характерной особенностью сегнетоэлектриков является своеобразная зависимость поляризации от напряженности внешнего электрического поля называемая петлей гистерезиса

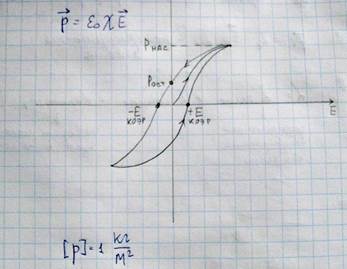
Е_коэр – поле, которое необходимо приложить, чтобы поляризация обратилась в ноль. Величины остаточной поляризации и коэрцитивной силы зависит не только от природы вещества образца но и так же от других факторов, таких как наличие примесей, размеры кристаллитов и термообработки внутри сегнетоэлектриков существуют сегнетоэлектрические домены. Внутри каждого домена поляризация совпадает с кристаллографическим направлением, и суммарная поляризация массивного куска материала представляет собой векторную сумму поляризации всех доменов. Причем вклад каждого отдельного домена поляризации образца пропорционален его объему

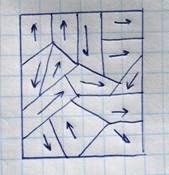
Если на такой образец воздействовать внешним электрическим полем, то будет происходить:1)поляризация может меняться по величине в каждом отдельном домене; 2)поляризация домена может менять свое направление; 3)наиболее выгодно ориентированный домены, то есть домены поляризации, которых составляет наименьший угол с направлением внешнего магнитного поля, могут увеличиваться в размерах за счет смещения границ между доменами. Спонтанная поляризация у сегнетоэлектриков сохраняется при повышении температуры до некоторой максимальной температуры называемой сегнетоэлектрической точкой Кюри. Это связанно с тем, что сильное тепловое движение атомов и молекул с повышением температуры является достаточным для разрушения эффекта направленного смещения ионов в соседних элементарных ячейках обуславливающих существование элементарного дипольного момента.

Магнитные свойства вещества

Магнитные характеристики вещества во многих отношениях формально сходны с его диэлектрическими характеристиками вещества. Например, наведенная магнитная поляризация (намагниченность) аналогична электрической поляризации. Существуют атомы и молекулы с постоянными магнитными диполями точно так же как существуют атомы и молекулы с постоянными электрическими диполями (полярные молекулы). Ряд материалов обладают спонтанной намагниченностью, такие материалы называются ферромагнетики, точно так же как некоторые материалы называются спонтанной поляризацией (сегнетоэлектрики). Необходимо, однако, отметить одно важное различие между магнитными и электрическими свойствами вещества. В природе существуют индивидуальные электрические заряды (монополи) которые могут быть как положительными так и отрицательными, соответствующих магнитных монополий, пока так называемых монополий Дирака. Все магнитные моменты обусловлены замкнутыми токами. Поместим в однородное магнитное поле с напряжённостью H и индукцией B однородное тело объемом V, это тело намагнитится и приобретет магнитный момент М, который является величиной векторной

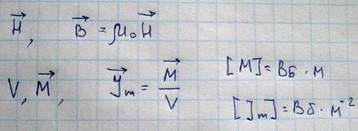
Магнитный момент на единицу объема – намагниченность.

В однородных магнетиках намагниченность направлена параллельно или антипараллельно внешнему магнитному полю

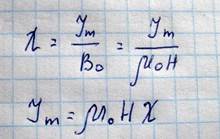
Намагниченное тело, то есть тело, находящееся во внешнем магнитном поле, создает собственное поле, которое в изотропных магнетиках вдали от его внешних границ может быть направленно параллельно или антипараллельно внешнему магнитному полю. Для изотропных магнетиков при этом суммарная индукция будет равна

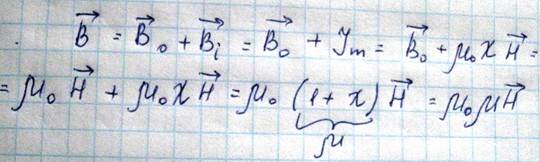
12.12.12

В зависимости от знака B₀=χ₀H и величины магнитной восприимчивости, все вещества в природе делятся на три большие группы: диамагнетики, парамагнетики, ферромагнетики.

Если χ<0, | χ |<1, то вещество называется диамагнетиком. Это вещество намагничивается против внешнего магнитного поля, следовательно оно втягивается в область сильного магнитного поля, и кроме того восприимчивость диамагнетика не зависит от напряженности внешнего магнитного поля и температуры

χ>0, | χ |<1 – такие тела намагничиваются в направлении действия внешнего магнитного поля, и, следовательно, втягиваются в область сильного магнитного поля (парамагнетики)

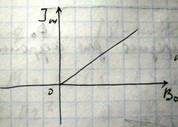
Линейная зависимость намагниченности от поля для парамагнетика выполняется только в области слабых магнитных полей и достаточно высоких температур. В случае низких температур и больших магнитных полей парамагнетики ведут себя следующим образом

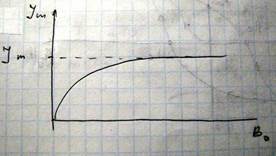
В отличие от диамагнетика восприимчивость парамагнетика зависит от температуры в соответствии с законом Кюри: χ=c/T.

χ>0, | χ |>1 - ферромагнетики, их восприимчивость положительна и выше единицы, и их восприимчивость зависит от внешнего магнитного поля

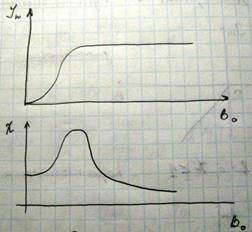
Процесс намагничивания ферромагнетиков характеризуется наличием петли гистерезиса, аналогично тому, как это выполняется для сегнетоэлектриков. Петля гистерезиса для ферромагнетика имеет следующий вид:

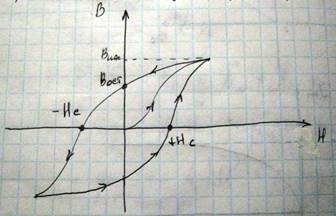
Площадь петли гистерезиса для ферромагнетика пропорциональна работе по перемагничиванию единицы объема материала, причем вся эта работа превращается в тепло, в результате чего при перемагничивании ферромагнетик нагревается. В зависимости от формы и площади петли гистерезиса ферромагнитные материалы делятся на мягкие и жесткие, или высококоэрцитивные. Магнитомягкие материалы используются для изготовления сердечников электрических машин и различных приборов, они обладают очень узкой петлей гистерезиса, то есть для них H_c мала, и кроме этого их магнитная восприимчивость, и, соответственно, проницаемость очень велика. Высококоэрцитивные материалы наоборот характеризуются большими значениями коэрцитивной силы и остаточным намагничиванием. Из них изготавливаются постоянные магниты. С повышением температуры магнитная восприимчивость, проницаемость, намагниченность уменьшаются и при некоторой температуре, называемой температурой Кюри, ферромагнитные свойства этих материалов исчезают, и они ведут себя как обычные парамагнетики, причем зависимость восприимчивости от температуры выглядит так χ=c/(T-θ_p) – Закон Кюри - Вейса. Парамагнитные температуры Кюри практические совпадающие с точкой Кюри. Монокристаллы ферромагнитных материалов характеризуются анизотропией намагничивания, то есть наличием в кристалле таких направлений, при воздействии поля вдоль которых насыщение намагниченности достигается при относительно небольших значениях магнитного поля - это называется анизотропией

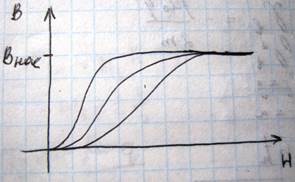три разных направления

Это характерно для анизотропных материалов. Технически важной особенностью ферромагнетиков в процессе их намагничивания является способность изменения размеров и формы, и это явление называется магнитострикцией. Оно лежит в основе создания магнитострикционных излучателей звука, используемых в геологии для звукового зондирования горных пород. Изучение природы магнетизма начнем с магнитных свойств атома. Здесь можно использовать модель строения атома по Бору, согласно которому, на примере атома водорода, электрон вращается вокруг ядра по круговой орбите

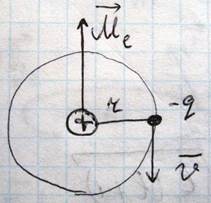
Электрон, вращающийся вокруг ядра, создает ток, величина которого I= -q*ν, где ν - частота обращения электрона, то есть число оборотов в единицу времени, магнитный момент этого тока

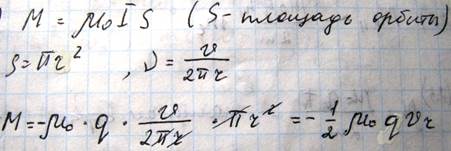
Магнитный момент электрона, обусловленный его движением по орбите, называется орбитальным магнитным моментом. Орбитальный магнитный момент направлен перпендикулярно плоскости орбиты электрона по правилу буравчика. Вместе с тем электрон, обращаясь по круговой орбите, обладает моментом импульса

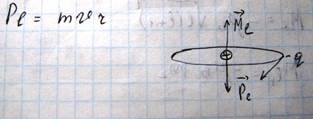
Он также перпендикулярен плоскости орбиты и направлен по правилу буравчика.

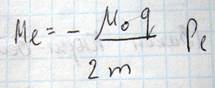
Гиромагнитное отношение M_l/P_l=γ_l=-μ₀q/2m

Как известно момент количества движения электрона в атоме квантуется, то есть принимает дискретное значение

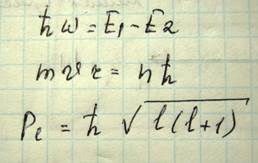
Квантуется также P_lh=m_lћ. Из этих соотношения сразу выходит вывод? что орбитальный момент электрона также квантуется

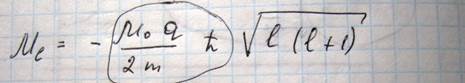
И квантуется также проекция магнитного момента

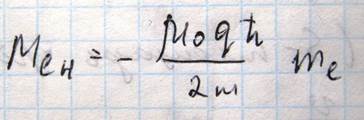
Выражение, стоящее перед скобкой, называется магнетон Бора

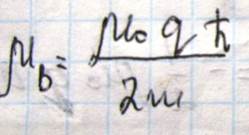
Магнетон бора представляет собой квант магнитного момента и принимается за единицу измерения магнитных моментов атомов

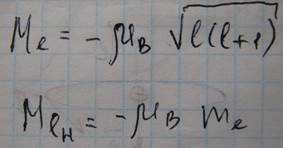
Для сложных атомов, электронная оболочка которых, состоит из многих электронов, результирующий орбитальный магнитный момент определяется путем суммирования орбитальных моментов отдельных электронов с учетом правила пространственного квантования, для полностью заполненных орбитальных оболочек равен нулю, и отличен только для незаполненных орбитальных оболочек

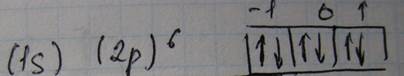
Помимо орбитального механического момента электрон обладает также собственным механическим моментом называемым спином

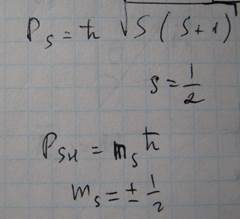
В связи с тем, что электрон обладает спином, то есть собственным механическим моментом, он также обладает собственным магнитным моментом и проекция собственного магнитного момента электрона на направление поля равна магнетону бора. Гиромагнитное отношение для механического момента электрона

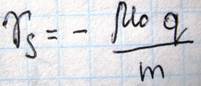
Как и в случае орбитальных магнитных моментов, результирующий спиновой магнитный момент заполненной оболочки равен нулю. Магнитный момент атома определяется не только магнитными моментами электрона, но также необходимо учитывать магнитный момент самого ядра, который, как известно, состоит из протонов и нейтронов, обладающих спином, равным ½. В связи с тем, что масса протонов нейтронов примерно в тысячу раз больше, соответствующий магнитный момент

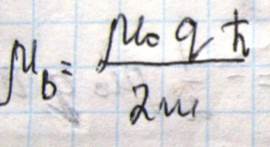
Рассмотрим теперь природу диамагнетизма. Диамагнетизм возникает вследствие изменения орбитального движения электронов под действием внешнего магнитного поля. Он присущ всем веществам, все вещества в природе диамагнитные, но часто перекрываются более сильными пара- и ферро- магнитными свойствами. В чистом виде диамагнетизм выявляется у веществ, результирующий магнитный момент которых равен нулю. То есть для веществ с заполненными электронными оболочками, рассмотрим движение электрона в атоме по орбите радиуса r

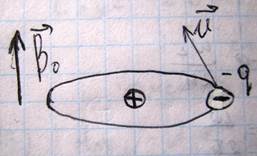
При отсутствии внешнего магнитного поля центростремительная сила, действующая на электрон будет равна

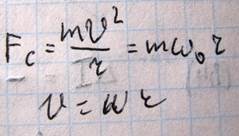
При наложении внешнего магнитно